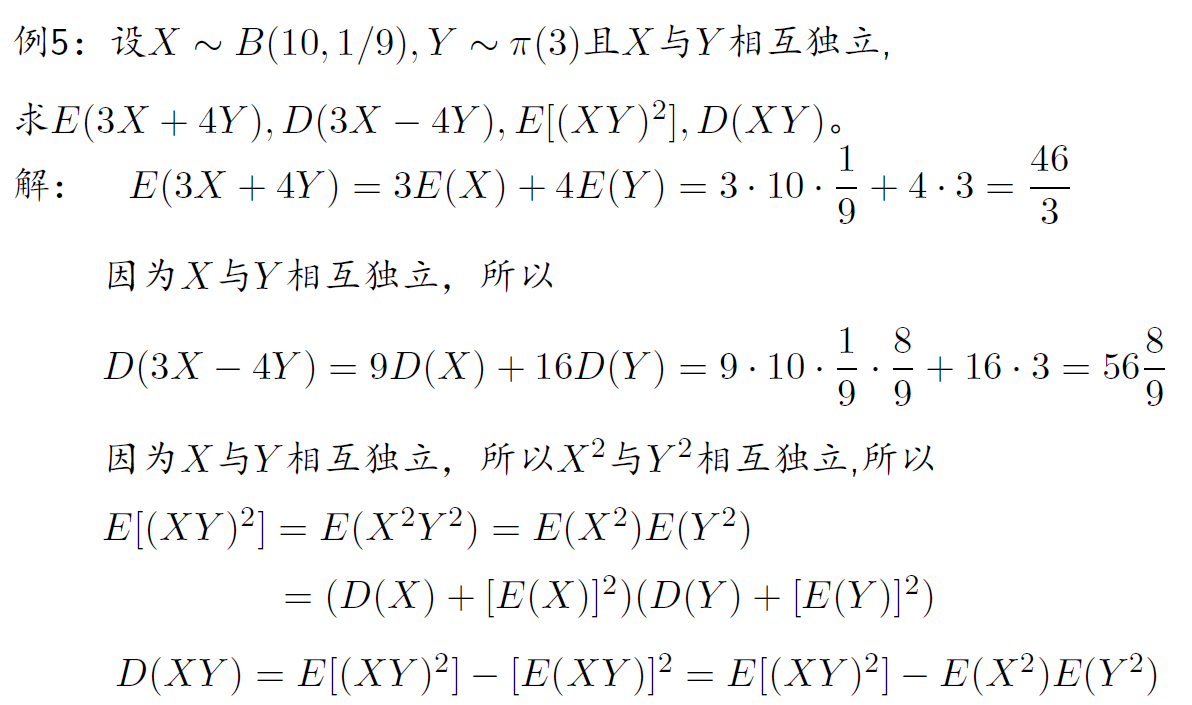随机变量的数字特征
定义:这些用来描述随机变量统 计特征的数字,称为随机变量的数字特征。
最常用的数字特征有:数学 期望(均值)、方差、相关系数和矩。
(Expectation)
设离散型随机变量X的分布律为P{X=xk}=pk,(k=1,2,…),若级数k=1∑∞xkpk绝对收敛,则称级数k=1∑∞xkpk的和为X的数学期望(均值),记为E(X);
设连续型随机变量X的概率密度为f(x),若积分∫−∞+∞xf(x)dx绝对收敛,则称级数∫−∞+∞xf(x)dx的和为X的数学期望(==均值==),记为E(X);
例

- E(C)=C
- E(CX)=CE(X)
- E(X+Y)=E(X)+E(Y)
- 若X与Y相互独立,则E(XY)=E(X)E(Y)
E(X)=p
E(X)=np
E(X)=λ
E(X)=2a+b
E(X)=λ1
E(X)=μ
-
X为离散型的,Y=g(X)的均值
若X的分布律为P{X=xi}=pi(i=1,2,…),则
E(Y)=i=1∑∞g(xi)pi
-
(X,Y)为离散型的,Z=g(X,Y)的均值
若(X,Y)的分布律为P{X=xi,Y=yi}=pi,j(i,j=1,2,…),则
E(Z)=i,j∑g(xi,yi)pi,j
-
X为连续型的,Y=g(X)的均值
若X的概率密度为fX(x),则
E(Y)=∫−∞+∞g(x)fX(x)dx
-
(X,Y)为连续型的,Z=g(X,Y)的均值
若(X,Y)的概率密度为f(x,y),则
E(Z)=∫−∞+∞∫−∞+∞g(x,y)f(x,y)dxdy
例



(Variance)
设X是一个对随机变量,若E{[X−E(X)]2}存在,则称其为X的方差,记为D(X)或Var(X)
称D(X)为标准差或均方差,记为σ(X)
D(X)=E(X2)−[E(X)]2
-
D(C)=0
-
D(CX)=C2D(X)
-
D(X+Y)=D(X)+D(Y)+2E{[X−E(X)][Y−E(Y)]}
若X,Y相互独立,则有D(X+Y)=D(X)+D(Y),又有D(X−Y)=D(X)+D(Y)
D(X)=p(1−p)
D(X)=np(1−p)
D(X)=λ
D(X)=12(b−a)2
D(X)=λ21
D(X)=σ2
| 分布名称 | 分布律或概率密度 | 数学期望 | 方差 |
|---|
| (0-1)分布 | P{X=k}=pk(1−p)1−k | p | p(1−p) |
| 二项分布 B(n,p) | P{X=k}=Cnkpk(1−p)n−k | np | np(1−p) |
| 泊松分布 π(λ) | P{X=k}=e−λk!λk | λ | λ |
| 均匀分布 U(a,b) | f(x)=⎩⎨⎧ b−a1a<x<b 0其他 | 2a+b | 12(b−a)2 |
| 指数分布 e(λ) | f(x)={ λe−λxx≥0 0其他 | λ1 | λ21 |
| 正态分布 N(μ,σ2) | f(x)=2πσ1e−2σ2(x−μ)2 | μ | σ2 |
例
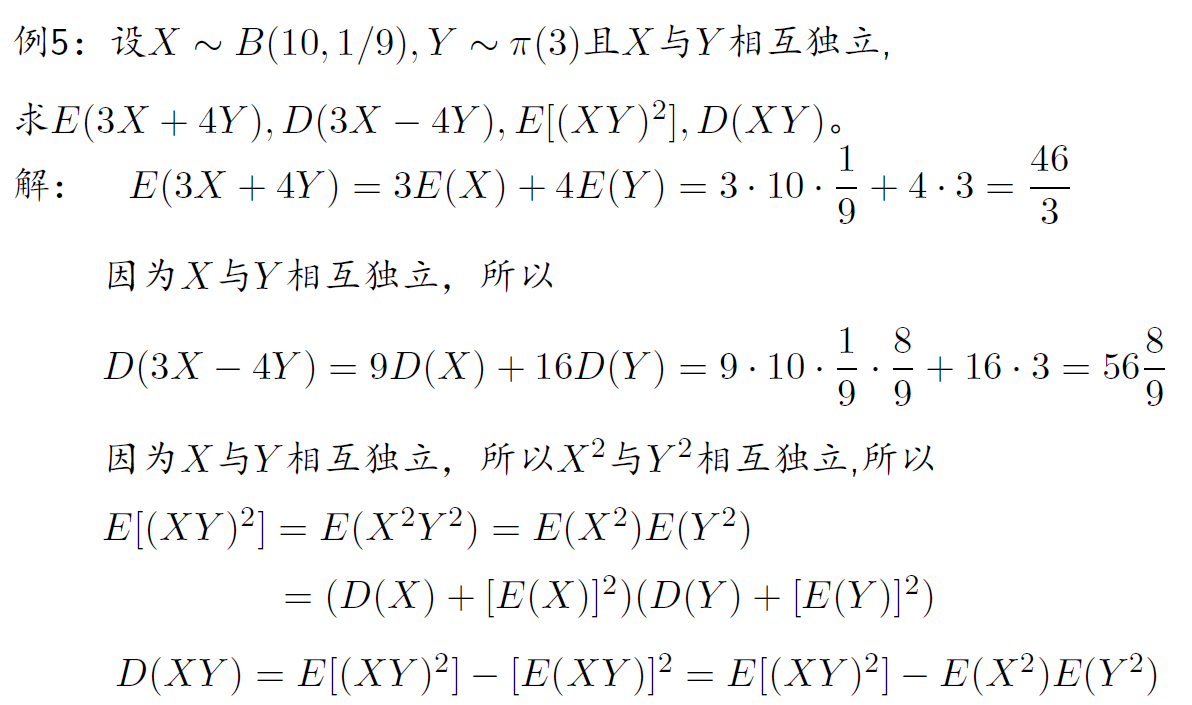
设(X,Y)为二维随机变量,若E{[X−E(X)][Y−E(Y)]}存在,则称其为X和Y的协方差,记为Cov(X,Y)
Cov(X,Y)=E(XY)−E(X)E(Y)
- Cov(X,X)=D(X)
- Cov(X,Y)=Cov(Y,X)
- Cov(aX,bY)=abCov(X,Y)
- Cov(C,X)=0
- Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)
- 当X与Y相互独立时,Cov(X,Y)=0
- D(aX+bY)=a2D(X)+b2D(Y)+2abCov(X,Y)
设(X,Y)为二维随机变量,D(X)>0,D(Y)>0,称
D(X)D(Y)Cov(X,Y)
为X和Y的相关系数,记为ρXY。其值为 0 时,X和Y不相关
-
∣ρXY∣≤1
-
当X与Y相互独立时,ρXY=0,X和Y不相关
-
若D(X)>0,D(Y)>0,∣ρXY∣=1⇔存在常数a,b,使得P{Y=aX+b}=1
而且当a>0时,ρXY=1,当a<0时,ρXY=−1
==相关系数刻画了随机变量X与Y之间”线性相关“的程度==
例
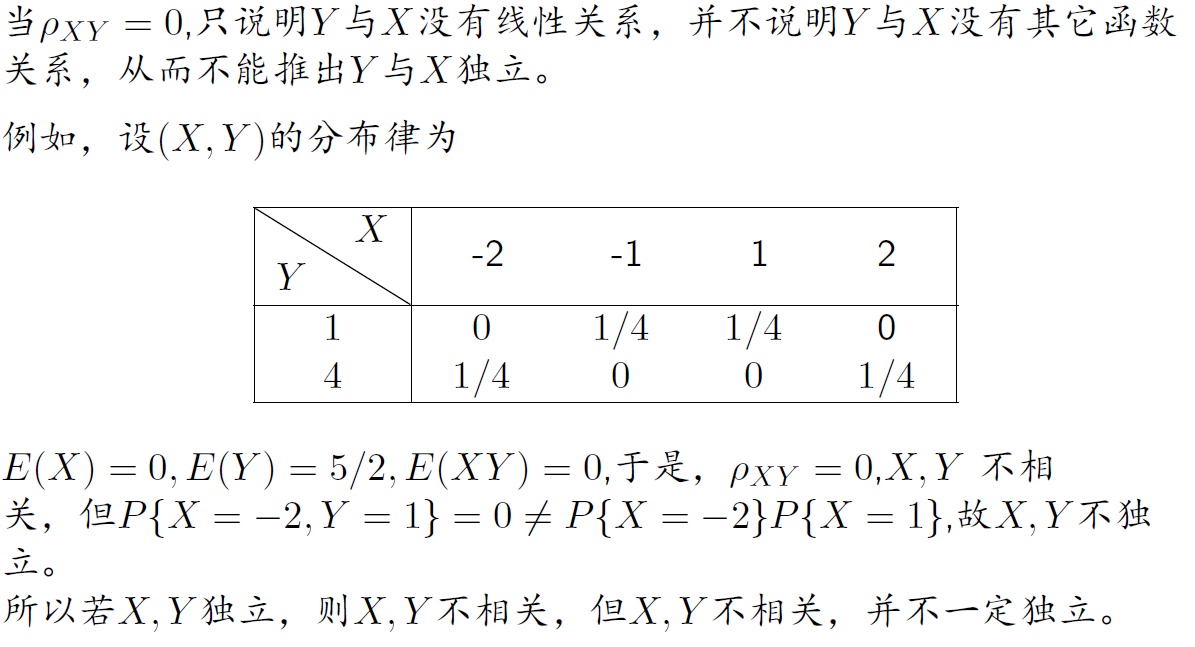
- X∗=DXX−E(X)是对随机变量X的标准化,有
ρXY=Cov(X∗,Y∗)
- 对于二维正态分布来说,不相关⇔独立
例


独立:没有任何关系
不相关:没有线性关系
独立⇒不相关不相关⇏独立
二维随机变量中,两者等价
设X,Y是随机变量
- 若E(Xk),k=1,2,…存在,称它为X的k阶原点矩,简称**k阶矩**
- 若E{[X−E(X)]k},k=2,3,…存在,称它为X的**k阶中心矩**
- 若E(XkYl),k,l=1,2,…存在,称它为X和Y的**k+l阶混合矩**
- 若E{[X−E(X)]k[Y−E(Y)]l},k,l=2,3,…存在,称它为**X和Y的k+l阶混合中心矩**
数学期望为一阶原点矩,方差为二阶中心矩,协方差为二阶混合中心矩
设n维随机变量(X1,X2,…,Xn)的二阶混合中心矩E{[Xi−E(Xi)][Yj−E(Yj)]}≜ci,j,(i,j=1,2,…,n)都存在,则称矩阵
c11c21⋮cn1c12c22⋮cn2……⋮…c1ncnn⋮cnn
为n维随机变量(X1,X2,…,Xn)的协方差矩阵