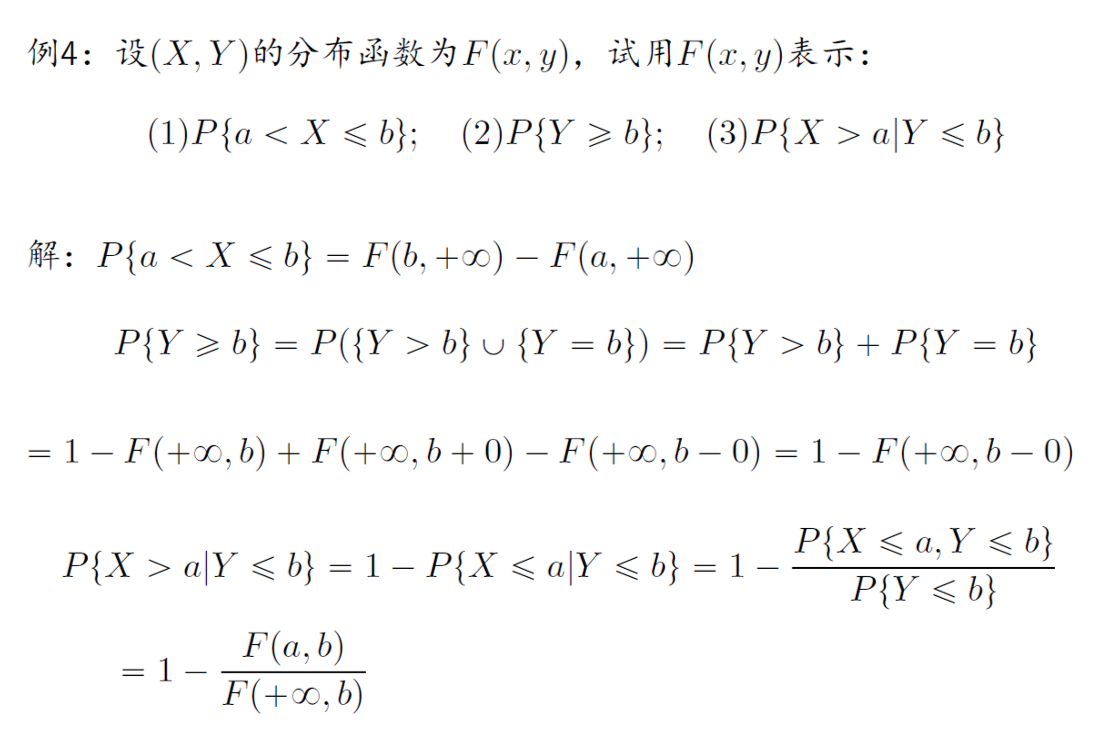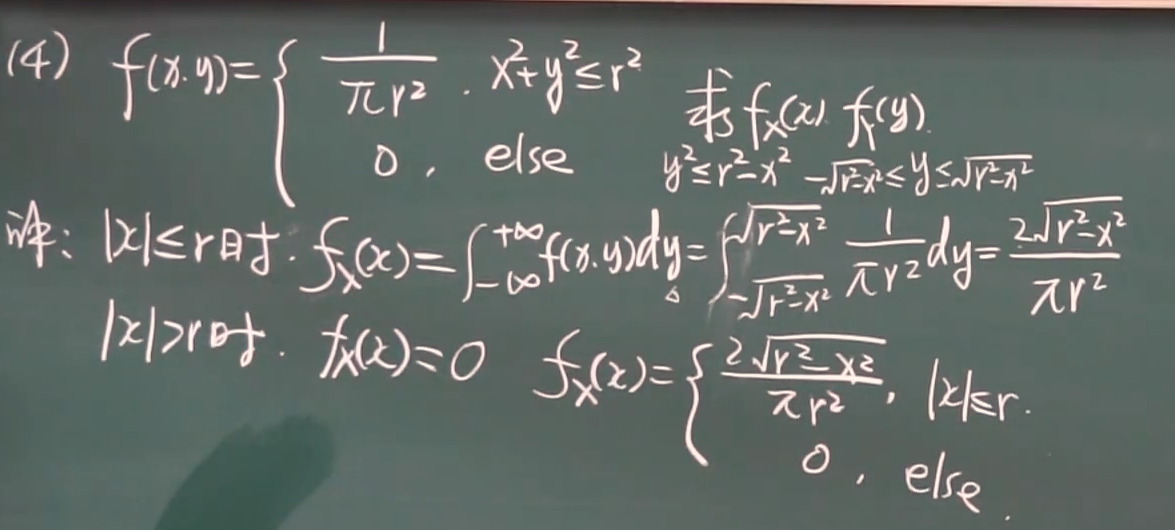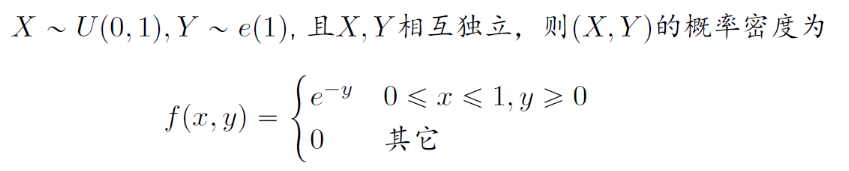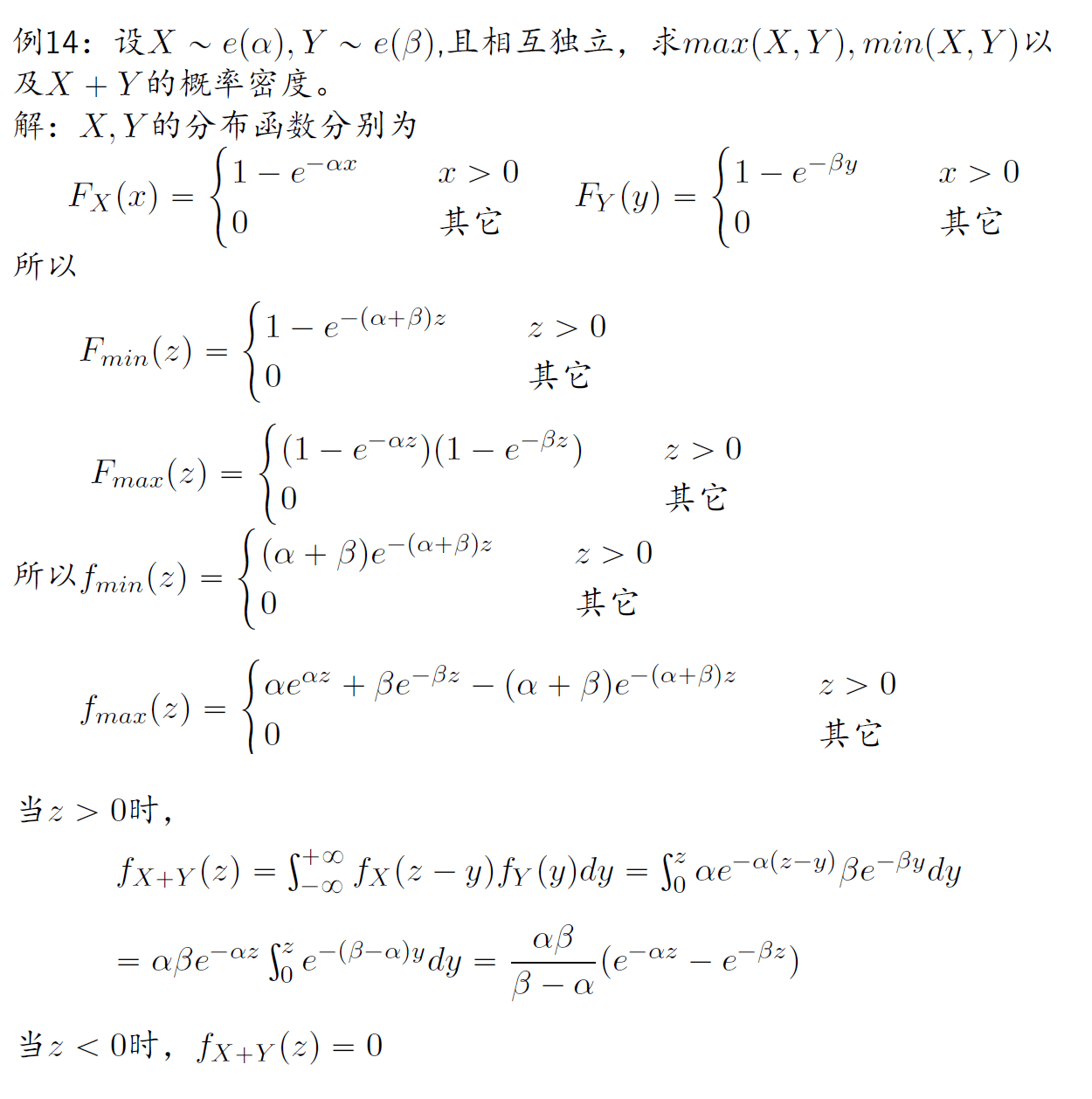多维随机变量及其分布
设E是一个随机试验,它的样本空间为S,设X=X(e),Y=Y(e)是定义在S上的两个随机变量,由它们构成的向量(X,Y),叫做二维随机变量(也称随机矢量)

设(X,Y)是一个二维随机变量,对任意的实数x,y,定义
F(x,y)=P({X≤x}∩{Y≤y})≜P{X≤x,Y≤y}
则称F(x,y)为二维随机变量(X,Y)的分布函数。
- 性质
- F(x,y)是关于变量 x 和 y 的不减函数
- 0≤F(x,y)≤1
- F(−∞,y)=x→−∞limF(x,y)=0,F(x,−∞)=y→−∞limF(x,y)=0F(−∞,−∞)=x,y→−∞limF(x,y)=0F(+∞,+∞)=x,y→+∞limF(x,y)=1
- F(x,y)既关于 x 右连续(F(x+0,y)=F(x,y)),也关于 y 右连续(F(x,y+0)=F(x,y))
若二维随机变量(X,Y)只有有限或可列个取值对,则称X,Y为一个二维离散型随机变量
若随机矢量(X,Y)所有可能取值对为(xi,yi),(i=1,2,…,j=1,2,…)
则称
P({X=xi}∩{Y=yi})≜{X=xi,Y=yi}=Pi,j(i=1,2,…,j=1,2,…)
为(X,Y)的分布律或称联合分布律。
联合分布律可以更直观地用以下表格的形式来描述

其中pi,j(i=1,2,…,j=1,2,…)要满足以下条件
- pi,j≥0
- i=1∑∞j=1∑∞pi,j=1

设(X,Y)为二维随机变量,F(x,y)为其分布函数,若存在一个非负二元
函数f(x,y),使得对任意x,y有
F(x,y)=∫−∞x∫−∞yf(s,t)dsdt
则称(X,Y)为二维连续型随机变量,并称f(x,y)为(X,Y)的概率密度,
或称为X和Y的联合概率密度
- f(x,y)≥0
- ∫−∞+∞∫−∞+∞f(x,y)dxdy=1
- P{(X,Y)∈D}=D∬f(x,y)dxdy(其中的D为一个平面区域)
- f(x,y)=∂x∂y∂2F(x,y)
(X,Y)的概率密度为
f(x,y)=⎩⎨⎧ A1(x,y)∈G 0其他其中G为平面上的一个有界区域,A为其面积(即S(G))
(X,Y)的概率密度为
f(x,y)=2π1−ρ2σ1σ21exp2(1−ρ2)−1[(σ1x−μ1)2−2ρ(σ1x−μ1)⋅(σ2y−μ2)+(σ2y−μ2)2]
记作(X,Y)∼N(μ1,μ2,σ12,σ22,ρ)
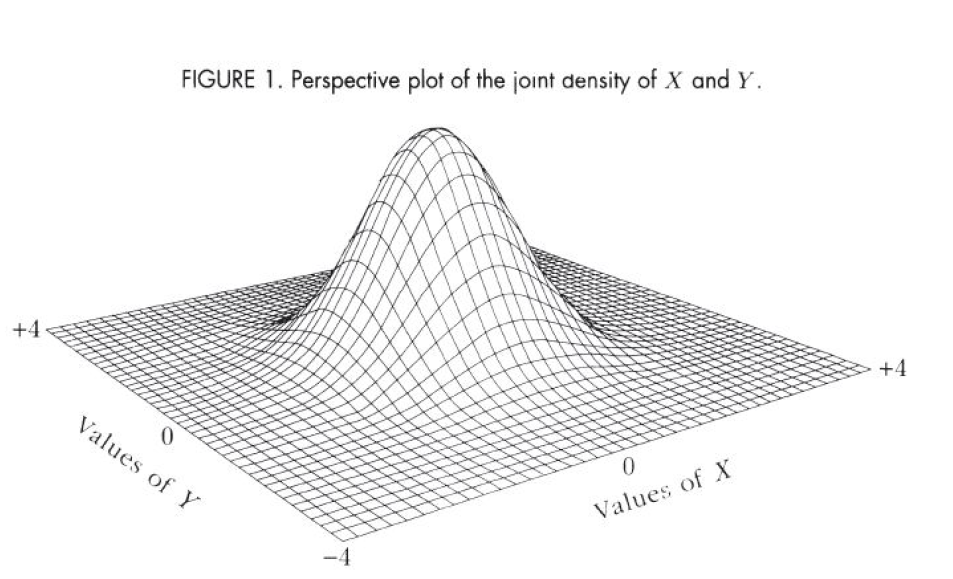


(Marginal Distribution)
对于二维随机变量 w(X,Y),其分布函数为 F(x,y),它的每个分量 X 和 Y 都是一维随机变量,它们各自的分布函数分别为 FX(x) 和 FY(y),通常把它们称为 (X,Y) 关于 X 和 Y 的边缘分布函数。
接下来我们考察一下联合分布函数F(x,y)与边缘分布函数FX(x)和FY(y)的关系:
FX(x)=P{X≤x}=P{X≤x,Y<+∞}=F(x,+∞)FY(y)=P{Y≤y}=P{X<+∞,Y≤y}=F(+∞,y)
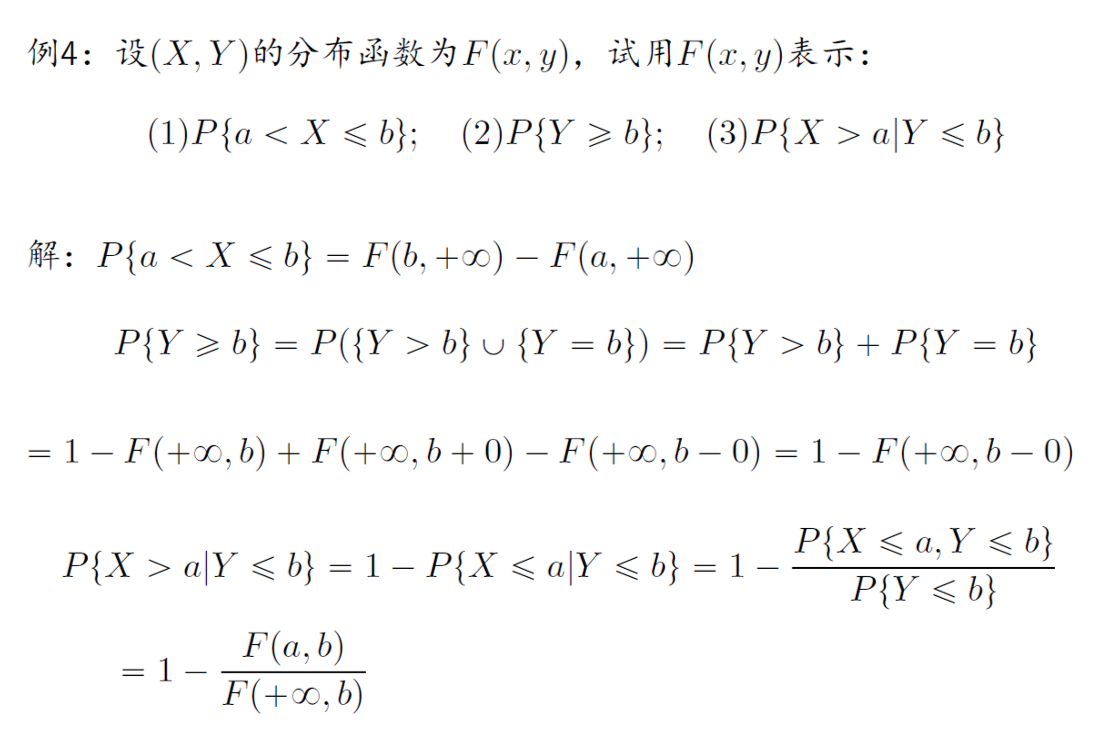 FX(x)=F(x,+∞)=xi≤x∑j=1∑+∞pi,j
FX(x)=F(x,+∞)=xi≤x∑j=1∑+∞pi,j
(注意:对一维随机变量X,FX(x)=xi≤x∑pi)
所以关于X的边缘分布律为
P{X=xi}=j=1∑∞pi,j≜pi⋅(i=1,2,…)
类似地,关于Y的边缘分布律为
P{Y=yi}=i=1∑∞pi,j≜pj⋅(j=1,2,…)

设二维连续型随机变量(X,Y)的联合概率密度为f(x,y),则
FX(x)=F(x,+∞)=∫−∞x[∫−∞+∞f(s,t)dt]ds对一维连续型随机变量X,FX(x)=∫−∞xfX(t)dt
所以,==关于X的边缘概率密度==为
fX(x)=∫−∞+∞f(x,y)dy
同样地,==关于 Y 的边缘概率密度==为
fY(y)=∫−∞+∞f(x,y)dx
例

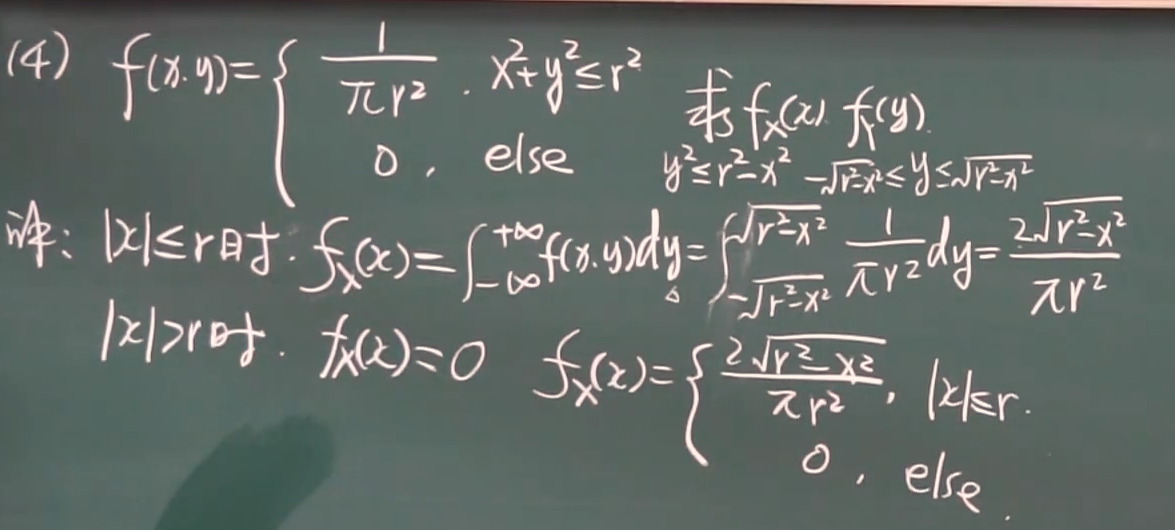
(Conditional Distribution)
设(X,Y)是二维离散型随机变量,其分布律为
P{X=xi,Y=yi}=pi,ji,j=1,2,…
的概率,即求事件
{X=xi∣Y=yi}i=1,2,…
的概率。由条件概率公式可得
P{X=xi∣Y=yi}=P{Y=yi}P{X=xi,Y=yi}=i=1∑∞pi,jpi,ji=1,2,…
其为在Y=yi的条件下随机变量X的==条件分布律==
类似地,称
P{Y=yi∣X=xi}=P{X=xi}P{X=xi,Y=yi}=j=1∑∞pi,jpi,jj=1,2,…
为在X=xi的条件下随机变量Y的条件分布律
考的不多
联合密度比边缘密度
称
fX∣Y(x∣y)=fY(y)f(x,y)
为在Y=y条件下X的==条件概率密度==,记为fX∣Y(x∣y)
同时称
FX∣Y(x∣y)=∫−∞xfY(y)f(s,y)ds=∫−∞xfX∣Y(x∣y)dx
为在Y=y条件下X的==条件分布函数==,记为FX∣Y(x∣y)或P{X≤x∣Y=y}
类似地,定义
fY∣X(y∣x)=fY(x)f(x,y)FY∣X(y∣x)=∫−∞yfX(x)f(x,t)dt
例


联合密度 = 边缘密度相乘
边缘密度 = 条件密度
设F(x,y),FX(x),FY(y)分别为二维随机变量(X,Y)的联合分布函数和边缘分布函数,若对任意的x,y,都有
F(x,y)=FX(x)FY(y)即P{X≤x,Y≤y}=P{X≤x}P{Y≤y}
==独立的条件==
- 离散型:P{X=xi,Y=yj}=P{X=xi}P{Y=yj} 对任意 i, j 成立
- 连续型:f(x,y)=fX(x)fY(y)
例
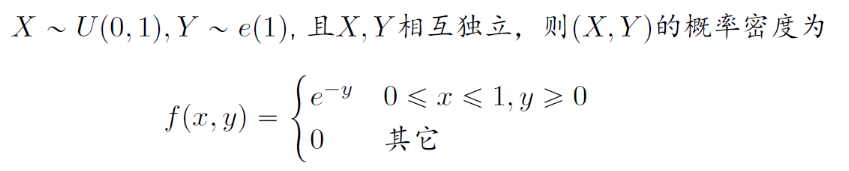
对于连续型随机变量(X,Y),若X与Y相互独立,当且仅当
fX(x)=fX∣Y(x∣y) 或 fY(y)=fY∣X(y∣x)
若(X,Y)∼N(μ1,μ2,σ12,σ22,ρ),��则
fX(x)=2πσ11e−2σ12(x−μ1)2,fX(x)=2πσ21e−2σ22(x−μ2)2
对于二维正态随机变量(X,Y),相互独立的充要条件为 ρ=0
n维随机变量(X1,X2,…,Xn)的分布函数定义为
F(x1,x2,…,xn)=P{X1≤x1,X2≤x2,…,Xn≤xn}
若对于所有x1,x2,…,xn,有
F(x1,x2,…,xn)=FX1(x1)FX2(x2)…FXn(xn)
则称X1,X2,…,Xn是相互独立的
设(X,Y)是二维随机变量,其概率密度为f(x,y),Z=g(X,Y)是一个二维随机变量的函数,==则==
FZ(z)=P{Z≤z}=P{g(X,Y)≤z}=Dz∬f(x,y)dxdy其中Dz={(x,y)∣g(x,y)≤z}
例

设(X,Y)是二维随机变量,其概率密度为f(x,y),则Z=X+Y的分布函数为
FZ(z)=∫−∞z[∫−∞+∞f(u−y,y)dy]du
其概率密度为
fX+Y(z)=∫−∞+∞f(z−y,y)dy=∫−∞+∞f(x,z−x)dx
例

设(X,Y)是二维随机变量,其概率密度为f(x,y),则Z=XY的分布函数为
fXY(z)=∫−∞+∞∣x∣f(x,xz)dx
也可以求得Z=XY的概率密度为
fXY(z)=∫−∞+∞∣x∣1f(x,xz)dx
设 (X,Y) 是二维随机变量,其概率密度为 f(x,y),则 M=max{X,Y} 的分布函数为
Fmax(z)=FX(z)FY(z)
N=min{X,Y} 的分布函数为
Fmin(z)=1−[1−FX(z)][1−FY(z)]
-
扩展
设Xi(i=1,2,…,n)是n个相互独立的随机变量,它们的分布函数为Fxi(x),则M=max{X1,X2,…,Xn}和N=min{X1,X2,…,Xn}的分布函数分别为
Fmax(z)=Fx1(z)Fx2(z)…Fxn(z)Fmin(z)=1−[1−Fx1(z)][1−Fx2(z)]…[1−Fxn(z)]
例
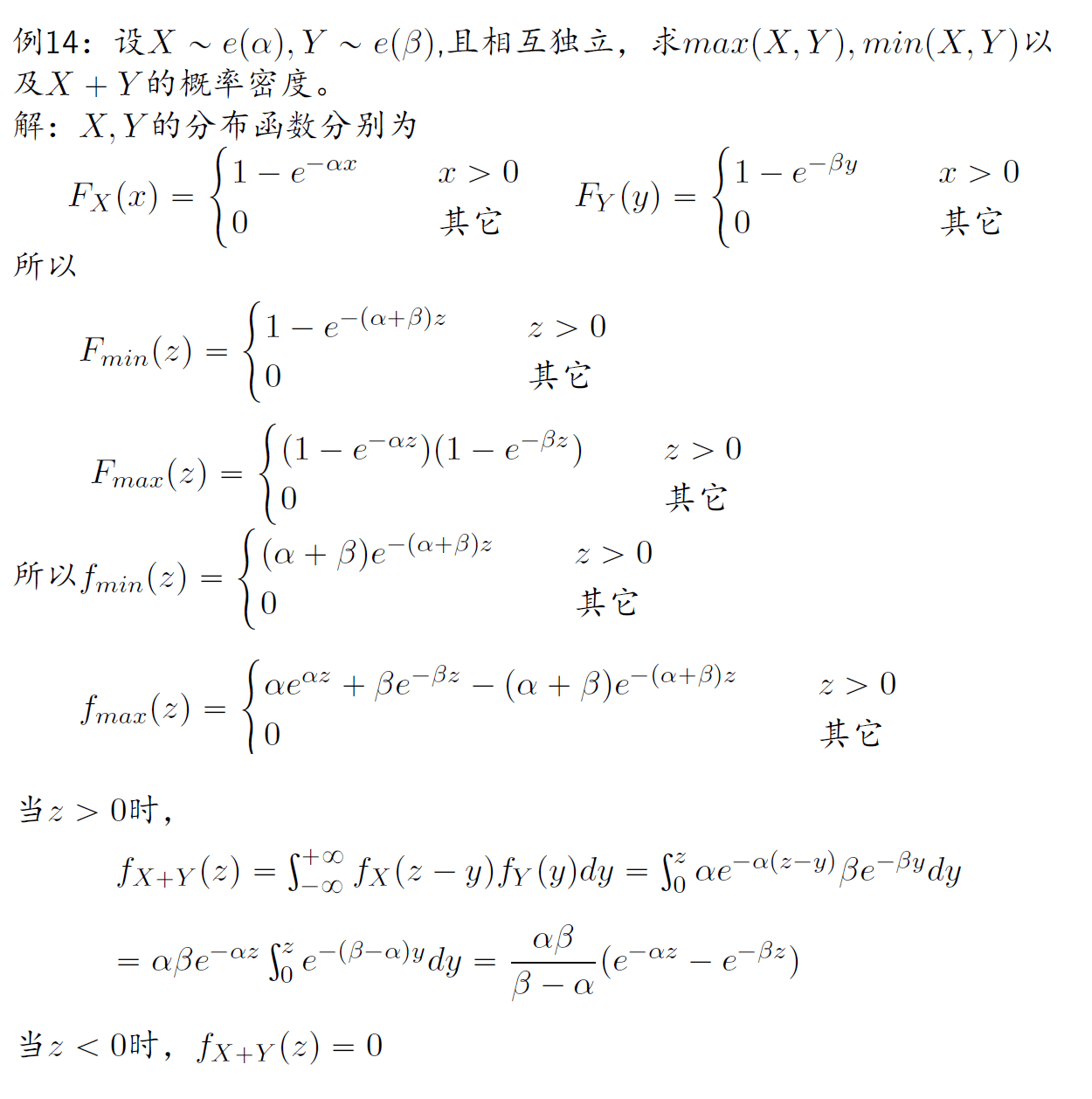
- 注意:若X和Y相互独立
- 若X∼N(μ1,σ12),Y∼N(μ2,σ22),则X+Y∼N(μ1+μ2,σ12+σ22)
- 若X∼e(α),Y∼e(β),则min(X,Y)∼e(α+β)
- 若X∼B(n1,p),Y∼B(n2,p),则Z=X+Y∼B(n1+n2,p)
- 若X∼π(λ1),Y∼π(λ2),则Z=X+Y∼π(λ1+λ2)