假设检验

引例

基本概念

理论性理解

假设

• 对未知总体分布的一个推断

• 关于总体分布类型的推断，叫非参数假设

• 关于总体分布参数的推断，叫参数假设

假设检验

• 检验假设正确与否
• 分参数假设检验与非参数假设检验
• 本章只关注参数假设检验

​

结合例子理解

在上例中，其中的 $H_0$ 称为原假设（零假设）

称$H_1$为备择假设，指原假设被拒绝后可供选择的假设

称给定的数 $\alpha$ 为显著水平

称 $Z=\cfrac{\overline X-\mu_0}{\sigma/\sqrt{n}}$ 为检验统计量

当检验统计量取某个区域$C$中的值时，就要拒绝原假设$H_0$，称区域$C$为拒绝域

称拒绝域的边界点为临界点

1. 由于决策是依据一次抽样作出的，在原假设$H_0$为真时，可能犯拒绝$H_0$的错误，称这种“弃真”错误为第一类错误

   其概率为$P\{拒绝 H_0|H_0 为真\}$，记为$P_{H_0}\{H_1\}$

2. 同时在原假设$H_0$不真时，可能犯接受$H_0$错误，称这种“取伪”的错误为第二类错误

   其概率为$P\{接受 H_0|H_1 为真\}$，记为$P_{H_1}\{H_0\}$

在样本容量一定时，若要使犯一类错误的概率减少，犯另一类错误的概率就会增加

显著性假设检验

控制犯第一类错误的概率的检验方法叫做显著性假设检验

步骤

1. 提出一个原假设$H_0$，和与此相对的备择假设$H_1$
2. 根据所做的假设，确定拒绝形式
3. 确定检验统计量，并由$P_{H_0}\{H_1\}\le \alpha$确定拒绝域
4. 通过抽样结果，作出拒绝域或接受$H_0$的决策（若检验统计量的观察值在拒绝域内，则拒绝$H_0$）

实际上，假设检验是一种带有概率意义的反证法

单个正态总体的假设检验

总体均值的假设检验

在总体方差$\sigma^2$已知的条件下

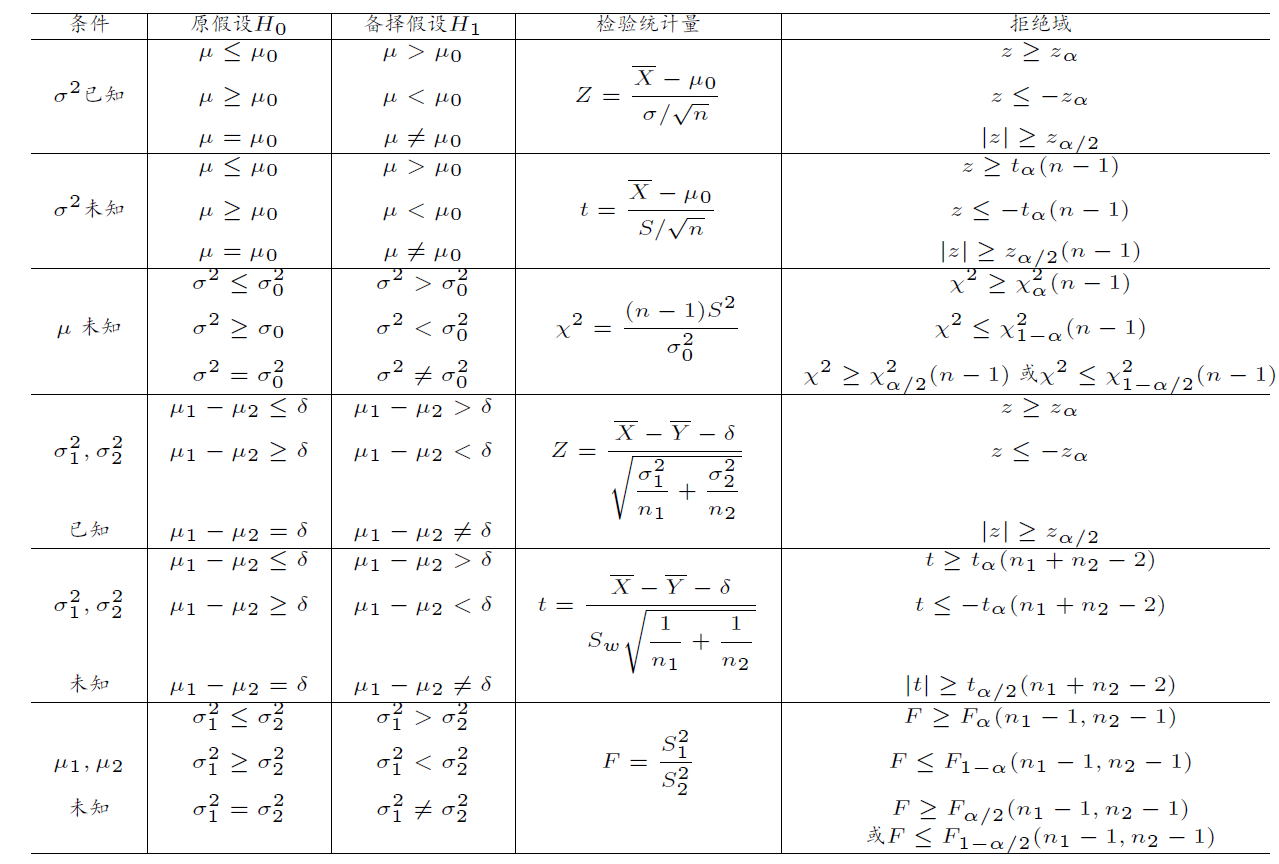
以$U=\cfrac{\overline X-\mu_0}{\sigma/\sqrt{n}}$为检验统计量，采用$z$检验法

• 双边检验：检验假设为$H_0:\mu=\mu_0,H_1:\mu\neq\mu_0$

$$拒绝域：|z|\ge z_{\alpha/2}$$

• 左边检验：检验假设为$H_0:\mu\ge\mu_0,H_1:\mu<\mu_0$

$$拒绝域：z\le -z_\alpha$$

• 右边检验：检验假设为$H_0:\mu\le\mu_0,H_1:\mu>\mu_0$

$$拒绝域：z\ge z_\alpha$$

在总体方差$\sigma^2$未知的条件下

以$T=\cfrac{\overline X-\mu_0}{S/\sqrt{n}}$为检验统计量，采用$t$检验法

• 双边检验：检验假设为$H_0:\mu=\mu_0,H_1:\mu\neq\mu_0$

$$拒绝域：|t|\ge t_{\alpha/2}(n-1)$$

• 左边检验：检验假设为$H_0:\mu\ge\mu_0,H_1:\mu<\mu_0$

$$拒绝域：t\le-t_{\alpha}(n-1)$$

• 右边检验：检验假设为$H_0:\mu\le\mu_0,H_1:\mu>\mu_0$

$$拒绝域：t\ge t_{\alpha}(n-1)$$

总体方差的假设检验

在$\mu$未知的条件下，以$\chi^2=\cfrac{(n-1)S^2}{\sigma_0^2}$为检验统计量，采用$\chi^2$检验法

• 双边检验：检验假设为$H_0:\sigma^2=\sigma_0^2,H_1:\sigma^2\neq\sigma_0^2$，拒绝域为

$$\chi^2\le\chi_{1-\alpha/2}^2(n-1) \ 或 \ \chi^2\ge\chi_{\alpha/2}^2(n-1)$$

• 左边检验：检验假设为$H_0:\sigma^2\ge\sigma_0^2,H_1:\sigma^2<\sigma_0^2$，拒绝域为

$$\chi^2\le\chi_{1-\alpha}^2(n-1)$$

• 右边检验：检验假设为$H_0:\sigma^2\le\sigma_0^2,H_1:\sigma^2>\sigma_0^2$，拒绝域为

$$\chi^2\le\chi_{\alpha}^2(n-1)$$

双正态总体的假设检验

总体均值差的检验

在总体方差$\sigma_1^2,\sigma_2^2$已知的条件下

以$Z=\cfrac{\overline{X_1}-\overline{X_2}-\delta}{\sqrt{\sigma_1^2/n_1+\sigma_2^2/n_2}}$为检验统计量，采用$z$检验法

• 双边检验：检验假设为$H_0:\mu_1-\mu_2=\delta,H_1:\mu_1-\mu_2\neq\delta$，拒绝域为

$$|z|\ge z_{\alpha/2}$$

• 左边检验：检验假设为$H_0:\mu_1-\mu_2\ge\delta,H_1:\mu_1-\mu_2<\delta$，拒绝域为

$$z\le-z_\alpha$$

• 右边检验：检验假设为$H_0:\mu_1-\mu_2\le\delta,H_1:\mu_1-\mu_2\delta$，拒绝域为

$$z\ge z_\alpha$$

在总体方差$\sigma_1^2,\sigma_2^2$未知的条件下

以$T=\cfrac{\overline{X_1}-\overline{X_2}-\delta}{S_w\sqrt{1/n_1+1/n_2}}$为检验统计量，采用$t$检验法

• 双边检验：检验假设为$H_0:\mu_1-\mu_2=\delta,H_1:\mu_1-\mu_2\neq\delta$，拒绝域为

$$|t|\ge t_{\alpha/2}(n_1+n_2-2)$$

• 左边检验：检验假设为$H_0:\mu_1-\mu_2\ge\delta,H_1:\mu_1-\mu_2<\delta$，拒绝域为

$$t\le-t_\alpha(n_1+n_2-2)$$

• 右边检验：检验假设为$H_0:\mu_1-\mu_2\le\delta,H_1:\mu_1-\mu_2>\delta$，拒绝域为

$$t\ge t_\alpha(n_1+n_2-2)$$

总体方差相等的假设检验

在$\mu_1,\mu_2$未知的条件下，以$F=\cfrac{S_1^2}{S_2^2}$为检验统计量，采用$F$检验法

• 双边检验：检验假设为$H_0:\sigma_1^2=\sigma_2^2,H_1:\sigma_1^2\neq\sigma_2^2$，拒绝域为

$$F\le F_{1-\alpha/2}(n_1-1,n_2-1) \ 或 \ F\ge F_{\alpha/2}(n_1-1,n_2-1)$$

• 左边检验：检验假设为$H_0:\sigma^2\ge\sigma_0^2,H_1:\sigma^2<\sigma_0^2$，拒绝域为

$$F\le F_{1-\alpha}(n_1-1,n_2-1)$$

• 右边检验：检验假设为$H_0:\sigma^2\le\sigma_0^2,H_1:\sigma^2>\sigma_0^2$，拒绝域为

$$F\ge F_{\alpha}(n_1-1,n_2-1)$$