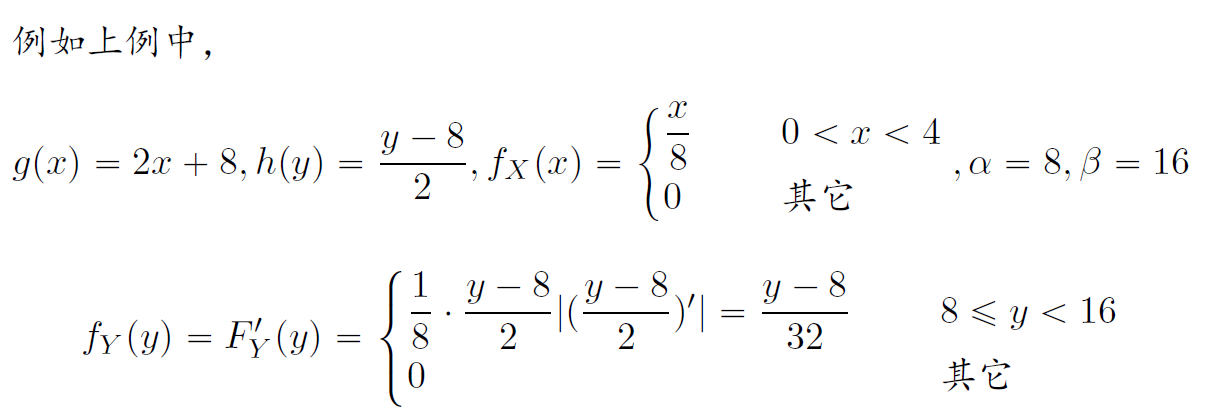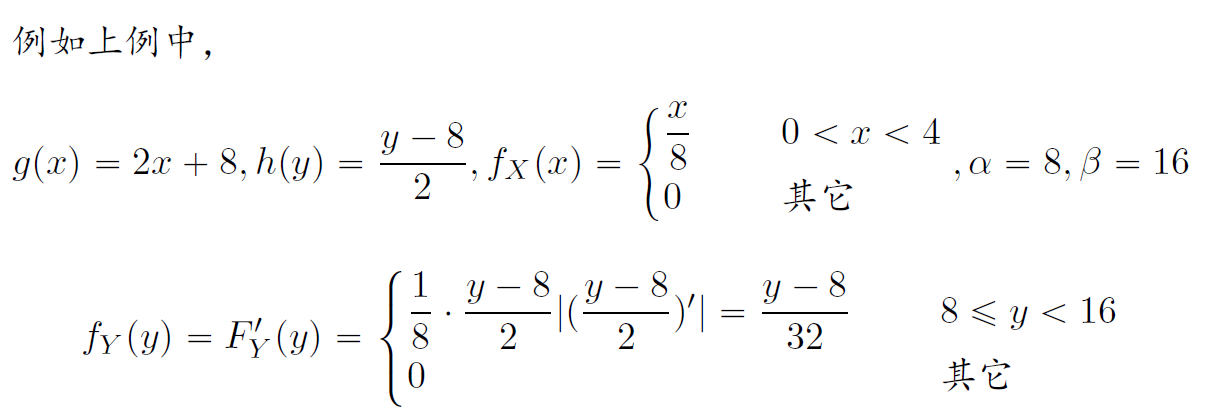随机变量及其分布
定义:设随机试验的样本空间为 S,把试验的每一个可能的结果 e∈S 与一 个
实数 X(e) 对应起来,则称这种定义在S上的一个实值单值映射 X=X(e) 为随机变量(Random Variables)
引入随机变量后,就可将对随机事件及其概率的研究转化为对随机变量及其取值规律的研究
设X为一个随机变量,如果它的全部可能取值只有有限个或可数无穷个,则称X为一个离散型随机变量
设离散型随机变量X所有可能取值为 xi(i=1,2,…,n或i=1,2,…),称P{X=xi}=pi(i=1,2,…,n或i=1,2,…)为X的概率分布或分布律
分布律可以更直观地用以下表格的形式来描述
| X | x1 | x2 | ... | xn | ... |
|---|
| pi | p1 | p2 | ... | pn | ... |
其中pi满足
- pi≥0
- i=1∑n(∞)pi=1
P{X=k}=pk(1−p)1−kk=0,1(0<p<1)
n 次实验发生了 k 次,每次实验独立,或是放回抽样
P{X=k}=Cnkpk(1−p)n−kk=0,1,2,…,n
记作 X∼B(n,p),X 即为即为 n 重贝努利试 验中 A 发生的次数
P{X=k}=e−λk!λkλ>0,k=0,1,2,…
记作 X∼π(λ)
例
- 某医院在一天的急诊病人数;
- 某一个时间间隔内某地区发生的交通事故的次数;
- 在一个时间间隔内某种放射性�物质发出经过计数器的α 粒子数
泊松定理:当 n 很大,p 很小时有近似式:
Cnkpk(1−p)n−k≈e−λk!λk
有时可将较难计算的二项分布转化为泊松分布去计算
补充:超几何分布
N 个样本中有 N1 类和 N2 类,从中(不放回地)取 n 个,取出 N1 的个数设为 k
P(X=k)=CNnCN1kCN2n−k
当 N 很大,n 很小时,不放回近似为放回,超几何分布近似为二项分布
-
某人进行射击,设每次射击的命中率为 0*.*02,独立射击 400 次,试求至少击中两次的概率
设击中的次数为 X,则 X∼B(400,0.02),因此所求概率为(近似为泊松定理计算)
P{X≥2}=1−P{X<2}=1−P{X=0}−P{X=1}=0.9972
-
某公司生产一种产品 300 件,废品率为 0*.*01,问在这 300 件产品中废品数大于 5 的概率是多少?
设 300 件产品中废品数为 X,则 X∼B(300,0.01),因此所求概率为
P{X≥5}=1−k=0∑5C300k(0.01)k(0.99)300−k≈1−k=0∑5k!e−33k=0.083918
设X是一个随机变量,x是任意实数,称函数
F(x)=P{X≤x}−∞<x<∞
为X的分布函数
-
P{X≤a}=F(a)
-
P{X>a}=1−F(a)
-
P{a<X≤b}=F(b)−F(a)
-
P{X=a}=F(a+0)−F(a−0)=F(a)−F(a−0)
注意,P{a≤X≤b}=F(b)−F(a),而是P{a≤X≤b}=F(b)��−F(a−0)
-
F(x)是一个不减函数
-
0≤F(x)≤1,且x→−∞limF(x)≜F(−∞)=0x→+∞limF(x)≜F(+∞)=1
-
F(x)是右连续的,即F(x+0)=F(x)
-
若一个函数具有以上性质,则它一定是某个随机变量的分布函数
设离散型随机变量X的分布律为P{X=xk}=pkk=1,2,…
则X的分布函数为(x 以内,分布函数为所有概率之和)
F(x)=P{X≤x}=xk≤x∑P{X=k}=xk≤x∑pk
即当xk−1≤x<xk时,F(x)=i−1∑k−1pi(在 x 附近,分布函数为其概率)
- 设随机变量X的分布函数为
F(x)=A+Barctanx,−∞<x<∞
试求:(1)系数A和B; (2)X落在(−1,1]内的概率
- 设随机变量X的分布律为
求X的分布函数,并求P{X≤21},P{23<X≤25}
解:前值为 1/4,后值为 1/2
如果对随机变量X的分布函数F(x),存在一个非负可积函f(x),使得对任意的x,��有
F(x)=P{X≤x}=��∫−∞xf(t)dt
则称X为一个连续型随机变量,称f(x)为X的概率密度函数,简称概率密度(Probability densities)
注:连续型随机变量的分布函数为连续函数,所以对任意a,有P{X=a}=0
- f(x)≥0
- ∫−∞+∞f(x)dx=1
- f(x)=F′(x)
P{X≤a}=∫−∞af(x)dx,P{X>b}=∫b+∞f(x)dxP{a<x≤b}=∫abf(x)dx
注意:分布函数与概率密度函数的区别,例如F(x)≤1成立,但f(x)≤1,∫−∞+∞F(x)dx=1不成立!
 f(x)=⎩⎨⎧ b−a1a<x<b 0其他
f(x)=⎩⎨⎧ b−a1a<x<b 0其他
记为X∼U(a,b)
分布函数
F(x)=⎩⎨⎧ 0x<ab−ax−aa≤x<b ax≥b
汽车站等车时间
针落地与某直线的倾斜角
f(x)={ λe−λxx≥0 0其他(λ>0)
记为X∼e(λ)
分布函数
F(x)={ 1−e−λxx>0 0其他
指数分布具有无记忆性,即
P{X>t}=p{X>s+t∣X>s}
新生的物品(生物)能存活 t 年的以上概率 = 已经活了 s 年的物品(生物)再存活 t 年以上的概率
电话系统通话时间
消耗性产品的寿命
生物寿命
f(x)=2πσ1e−2σ2(x−μ)2,−∞<x<+∞
记为X∼N(μ,σ2)
性质
-
μ 为均值,控制图像位置,σ 为方差,控制图像高低(陡缓)
-
y=f(x) 以 x=μ 为对称轴,呈钟形曲线
-
概率最大值在 x=μ 时取到,值为 2πσ1
分布函数
F(x)=2πσ1∫−∞xe−2σ2(t−μ)2dt
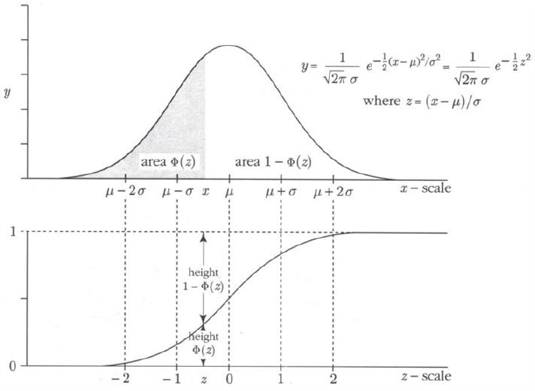
对正态分布随机变量X,若μ=0,σ=1,则称X服从标准正态分布,其分布函数和概率密分别用Φ(x)和ϕ(x)表示,即
Φ(x)=2π1∫−∞xe−2t2dt,ϕ(x)=2π1e−2x2Φ(0)=21,Φ(x)=1−Φ(−x)
-
定理 1:设X∼N(μ,σ2),则Y=σX−μ N(0,1)。因此有(标准化)
- P{X≤a}=P{σX−μ≤σa−μ}=Φ(σa−μ)
- P{X>b}=P{σX−μ>σb−μ}=1−Φ(σb−μ)
- P{a<X≤b}=P{ σa−μ<σX−μ≤σb−μ}=Φ(σb−μ)−Φ(σa−μ)
当a>0时,Φ(a)的值往往是通过查表得到,当a<0时,先利用Φ(a)=1−Φ(−a),再查表得到。
p{∣x−μ∣<σ}=0.6826
p{∣x−μ∣<2σ}=0.9544
p{∣x−μ∣<3σ}=0.9974
-
某元件的寿命X服从指数分布,其参数为λ=10001,求 3 个这样的元件用 1000 小时时,至少已有一个损坏的概率
解:一个元件使用 1000 小时时损坏的概率为
P{X≤1000}=1−e−1
用Y表示 3 个元件中使用 1000 小时时损坏的元件数,则Y∼B(3,1−e−1),因此所求概率为
P{Y≥1}=1−P{Y=0}=1−C30(1−e−1)0(e−1)3=1−e−3
-
设X∼N(1,4)
(1)求P{x≤5}, P{0<X≤1.6}, P{∣X−1∣≤2}
(2)设d满足P{X>d}≥0.9,问d至少为多少
解:
(1)标准化,查表。
如果存在一个函数g(⋅),使得随机变量X,Y满足:Y=g(X),则称随机变量Y是随机变量X的函数。
设离散型随机变量X的分布律为:
P{X=xi}=pi,i=1,2,…
显然,X的随机变量函数Y=g(X)也是离散型随机变量,且Y的分布律为
P{Y=yi}=g(xi)=yi∑pij=1,2,…
设X的概率密度为fX(x),Y=g(X),则Y的分布函数为
FY(y)=P{Y≤y}=P{g(X)≤y}=∫Cyf(x)dx
其中Cy={x∣g(x)≤y}
方法:FY(x)→FX(x),两边求导,fY(x)←fX(x)

-
定理
设随机变量X概率密度为fX(x),函数y=g(x)处处可导,且g′(x)>0(或g′(x)<0),则Y=g(X)也是连续型随机变量,其概率密度为
fY(y)={ fX(h(y))∣h′(y)∣α<y<β 0其他
其中x=h(y)为y=g(x)的反函数
当f(x)在(−∞,+∞)上非零时
α=min(g(−∞),g(+∞)),β=max(g(−∞),g(+∞))
当f(x)在[a,b]上非零时
α=min(g(a),g(b)),β=max(g(a),g(b))