跳到主要内容

参数估计

统计推断的基本问题分为两类：一是估计问题，另一个是假设检验。本章主要讨论总体参数的点估计和区间估计。

点估计​

用总体 X\Bbb X 的一个样本来估计总体未知参数的方法称为点估计法

术语​

设 X1,X2,…,XnX_1,X_2,\ldots,X_n 是来自总体 X\Bbb X 的一个样本，点估计法就是要构建一个合适的统计量θ^(X1,X2,…,Xn)\hat{\theta}(X_1,X_2,\ldots,X_n)用它的观察值θ^(x1,x2,…,xn)\hat{\theta}(x_1,x_2,\ldots,x_n)作为未知参数θ\theta的近似值，有

  • 估计量：θ^(X1,X2,…,Xn)\hat{\theta}(X_1,X_2,\ldots,X_n)

  • 估计值：θ^(x1,x2,…,xn)\hat{\theta}(x_1,x_2,\ldots,x_n)

估计量和估计值统称为估计

矩估计法​

用样本矩作为相应的总体矩的估计方法称为矩估计法

image-20210223095556527

方法​

设θ1,θ2,…,θk\theta_1,\theta_2,\ldots,\theta_k为带估计的参数，用Θ\Theta表示带估计参数组成的向量，即Θ=(θ1,θ2,…,θk)\Theta=(\theta_1,\theta_2,\ldots,\theta_k)

  • X\Bbb X 为连续型总体，其概率密度为 f(x,Θ)f(x,\Theta)，总体的前 kk 阶矩为
μl(Θ)=E(Xl)=∫−∞+∞xlf(x,Θ)dxl=1,2,…,k\mu_l(\Theta)=E(X^l)=\int_{-\infty}^{+\infty}x^lf(x,\Theta)dx\quad l=1,2,\ldots,k
  • X\Bbb X 为离散型总体，其分布律为 P{X=xi}=pi(Θ),i=1,2,…,kP\{X=x_i\}=p_i(\Theta),i=1,2,\ldots,k，总体的前 kk 阶矩为
μl(Θ)=E(Xl)=∑i=1∞(xi)lpi(Θ)l=1,2,…,k\mu_l(\Theta)=E(X^l)=\sum\limits_{i=1}^{\infty}(x_i)^lp_i(\Theta)\quad l=1,2,\ldots,k

设X1,X2,…,XnX_1,X_2,\ldots,X_n为来自总体X\Bbb X的一个样本，它的前kk阶样本矩观察值为

al=1n∑i=1nxil(l=1,2,…,k)a_l=\cfrac{1}{n}\sum\limits_{i=1}^nx_i^l\quad (l=1,2,\ldots,k)

然后列方程（组）

{ μ1(θ1,θ2,…,θk)=a1 μ2(θ1,θ2,…,θk)=a2 ⋮ μk(θ1,θ2,…,θk)=ak\begin{cases} \ \mu_1(\theta_1,\theta_2,\ldots,\theta_k)=a_1 \\ \ \mu_2(\theta_1,\theta_2,\ldots,\theta_k)=a_2 \\ \ \vdots \\ \ \mu_k(\theta_1,\theta_2,\ldots,\theta_k)=a_k \end{cases}

最后求解方程（组），即可获得未知参数θ1,θ2,…,θk\theta_1,\theta_2,\ldots,\theta_k的估计值为

θ^l=θl(a1,a2,…,ak)(l=1,2,…,k)\hat{\theta}_l=\theta_l(a_1,a_2,\ldots,a_k)\quad (l=1,2,\ldots,k)

因此估计量为

θ^l=θl(A1,A2,…,Ak)(l=1,2,…,k)\hat{\theta}_l=\theta_l(A_1,A_2,\ldots,A_k)\quad (l=1,2,\ldots,k)

例​

image-20210106112859958 image-20210111100234564

结论​

  1. 总体期望可以由样本均值（一阶中心矩）表示，X‾或A1\overline{X} 或 A_1
  2. 总体方差可以由样本二阶中心矩表示，A2A_2

最大似然估计法​

设 θ1,θ2,…,θk\theta_1,\theta_2,\ldots,\theta_k 为带估计的参数，用Θ\Theta表示带估计参数组成的向量，即Θ=(θ1,θ2,…,θk)\Theta=(\theta_1,\theta_2,\ldots,\theta_k)

设x1,x2,…,xnx_1,x_2,\ldots,x_n是一组抽样值，这意味着{X1=x1,X2=x2,…,Xn=xn}\{X_1=x_1,X_2=x_2,\ldots,X_n=x_n\}是一个大概率事件。

最大似然估计法就是要确定未知参数的值，使得P{X1=x1,X2=x2,…,Xn=xn}P\{X_1=x_1,X_2=x_2,\ldots,X_n=x_n\}（这其中含有未知参数）为最大。

方法​

  • X\Bbb X 为离散型总体，其分布律为 P{X=xi}=pi(Θ),i=1,2,…,kP\{X=x_i\}=p_i(\Theta),i=1,2,\ldots,k，设x1,x2,…,xnx_1,x_2,\ldots,x_n是一组抽样值
P{X1=x1,X2=x2,…,Xn=xn}=∏i=1npi(Θ),令L(x1,x2,…,xn;Θ)=∏i=1npi(Θ)P\{X_1=x_1,X_2=x_2,\ldots,X_n=x_n\}=\prod\limits_{i=1}^np_i(\Theta),令\\ L(x_1,x_2,\ldots,x_n;\Theta)=\prod\limits_{i=1}^np_i(\Theta)
  • X\Bbb X 为连续型总体，其概率密度为 f(x,Θ)f(x,\Theta)，设x1,x2,…,xnx_1,x_2,\ldots,x_n是一组抽样值
P{X1=x1,X2=x2,…,Xn=xn}≈∏i=1nf(xi;Θ)P\{X_1=x_1,X_2=x_2,\ldots,X_n=x_n\}\approx\prod\limits_{i=1}^nf(x_i;\Theta)

​ 其中∏i=1ndxi\prod\limits_{i=1}^ndx_i与未知参数Θ\Theta无关

L(x1,x2,…,xn;Θ)=∏i=1nf(xi;Θ)L(x_1,x_2,\ldots,x_n;\Theta)=\prod\limits_{i=1}^nf(x_i;\Theta)

称

L=(x1,x2,…,xn;θ1,θ2,…,θk)L=(x_1,x_2,\ldots,x_n;\theta_1,\theta_2,\ldots,\theta_k)

为似然函数，其自变量为θ1,θ2,…,θk\theta_1,\theta_2,\ldots,\theta_k。

最大似然估计就是要确定参数取何值时似然函数达到最大值。

通常利用对数似然函数来求，即求

∂∂θilnL(x1,x2,…,xn;θ1,θ2,…,θk)=0(i=1,2,…,k)\cfrac{\partial}{\partial\theta_i}lnL(x_1,x_2,\ldots,x_n;\theta_1,\theta_2,\ldots,\theta_k)=0\qquad(i=1,2,\ldots,k)

来求得未知参数的估计值θ^1,θ^2,…,θ^k\hat\theta_1,\hat\theta_2,\ldots,\hat\theta_k，再将其估计值改为估计量

例​

image-20210111102238736

步骤​

  1. 求总体的分布律/概率密度
  2. 写出似然函数
L(Θ)=∏i=1npi(Θ)或L(Θ)=∏i=1nf(xi;Θ)L(\Theta)=\prod\limits_{i=1}^np_i(\Theta)\\ 或 \\ L(\Theta)=\prod\limits_{i=1}^nf(x_i;\Theta)
  1. 取对数，求导
∂∂ΘlnL=...\cfrac{\partial}{\partial\Theta}lnL=...

估计量的评选标准​

无偏性​

若估计量 θ^=θ^(X1,X2,…,Xn)\hat\theta=\hat\theta(X_1,X_2,\ldots,X_n) 的数学期望 E(θ^)E(\hat\theta) 存在，且对任意 θ∈Θ\theta\in \Theta 有

E(θ^)=θE(\hat\theta)=\theta

则称θ^\hat\theta是θ\theta的无偏估计量

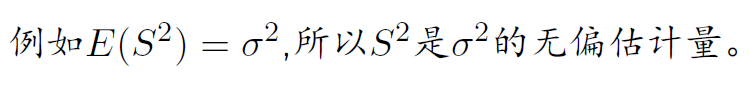
image-20210111102716666

有效性​

设θ^1=θ^1(X1,X2,…,Xn)\hat\theta_1=\hat\theta_1(X_1,X_2,\ldots,X_n)与θ^2=θ^2(X1,X2,…,Xn)\hat\theta_2=\hat\theta_2(X_1,X_2,\ldots,X_n)都是θ\theta的无偏估计量，若对任意的θ∈Θ\theta\in \Theta，有

D(θ^1)≤D(θ^2)D(\hat\theta_1)\le D(\hat\theta_2)

则称 θ^1\hat\theta_1 较 θ^2\hat\theta_2 有效

image-20210111103649707

相合性​

设 θ^=θ^(X1,X2,…,Xn)\hat\theta=\hat\theta(X_1,X_2,\ldots,X_n) 是参数 θ\theta 的估计量，若对于任意的 θ∈Θ\theta\in \Theta，对于任意 ε>0\varepsilon>0 有

lim⁡n→∞P{∣θ^−θ∣<ε}=1\lim\limits_{n\rightarrow\infty}P\{|\hat\theta-\theta|<\varepsilon\}=1

则称 θ^\hat\theta 是 θ\theta 的相合估计量

image-20210111104315266

区间估计​

置信区间​

设总体 X\Bbb X 的分布含有一个未知参数 θ\theta，对于给定的 α(0<α<1)\alpha(0<\alpha<1)，由来自 X\Bbb X 的样本 X1,X2,…,XnX_1,X_2,\ldots,X_n 确定的两个统计量θ‾=θ‾(X1,X2,…,Xn)\underline\theta=\underline\theta(X_1,X_2,\ldots,X_n) 和 θ‾=θ‾(X1,X2,…,Xn)\overline\theta=\overline\theta(X_1,X_2,\ldots,X_n)，对任意 θ∈Θ\theta\in\Theta 都有

P{θ‾<θ<θ‾}≥1−αP\{\underline\theta<\theta<\overline\theta\}\ge 1-\alpha

则称随机区间 (θ‾,θ‾)(\underline\theta,\overline\theta)为 θ\theta 的一个置信水平为 1−α1-\alpha 的置信区间，

  • θ‾\underline\theta：双侧置信下限

  • θ‾\overline\theta：双侧置信上限

  • 1−α1-\alpha：置信水平

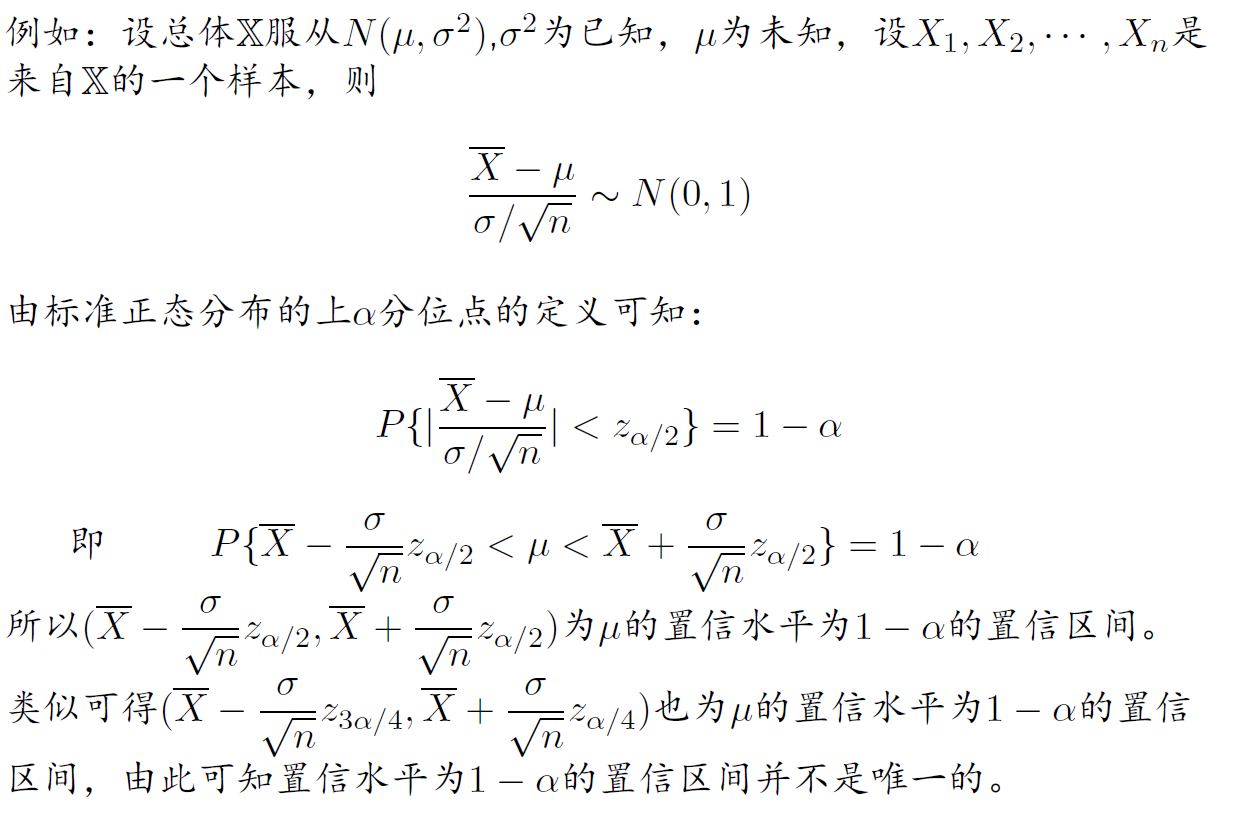
image-20210113101008116

区间估计​

求出一个合适的置信水平为 1−α1-\alpha 的置信区间，使得该区间包含参数 θ\theta 真值的可信程度为置信水平 1−α1-\alpha

步骤​

  1. 寻求一个样本 X1,X2,…,XnX_1,X_2,\ldots,X_n 和 θ\theta 的函数 W=W(X1,X2,…,Xn,θ)W=W(X_1,X_2,\ldots,X_n,\theta)，使其分布是已知（但该分布与θ\theta无关），（通常称这个WW为枢轴量）
  2. 对给定的置信水平 1−α1-\alpha，由双侧分位点确定 aa 和 bb，使得
P{a<W(X1,X2,…,Xn,θ)<b}=1−αP\{a<W(X_1,X_2,\ldots,X_n,\theta)<b\}=1-\alpha
  1. 由 a<W(X1,X2,…,Xn,θ)a<W(X_1,X_2,\ldots,X_n,\theta) 得出 θ‾<θ<θ‾\underline\theta<\theta<\overline\theta，则 (θ‾,θ‾)(\underline\theta,\overline\theta) 为所求的 θ\theta 的置信水平为 1−α1-\alpha 的置信区间

正态总体均值与方差的区间估计​

单个总体的情况​

  1. 方差σ2\sigma^2已知的条件下均值μ\mu的置信区间（略）
  2. 方差σ2\sigma^2未知的条件下均值μ\mu的置信区间
(X‾±Sntα/2(n−1))(\overline X\pm\cfrac{S}{\sqrt{n}}t_{\alpha/2}(n-1))
  1. 方差σ2\sigma^2的置信区间
((n−1)S2χα/22(n−1),(n−1)S2χ1−α/22(n−1))(\cfrac{(n-1)S^2}{\chi^2_{\alpha/2}(n-1)},\cfrac{(n-1)S^2}{\chi^2_{1-\alpha/2}(n-1)})

两个总体的情况​

  1. σ12,σ22\sigma_1^2,\sigma_2^2已知，μ1−μ2\mu_1-\mu_2的区间估计，枢轴量为
Z=X‾−Y‾−(μ1−μ2)σ12n1+σ22n2∼N(0,1)Z=\cfrac{\overline X-\overline Y-(\mu_1-\mu_2)}{\sqrt{\cfrac{\sigma_1^2}{n_1}+\cfrac{\sigma_2^2}{n_2}}}\sim N(0,1)
  1. σ12,σ22\sigma_1^2,\sigma_2^2未知，μ1−μ2\mu_1-\mu_2的区间估计，枢轴量为
t=X‾−Y‾−(μ1−μ2)Sw1n1+1n2∼t(n1+n2−2)t=\cfrac{\overline X-\overline Y-(\mu_1-\mu_2)}{S_w\sqrt{\cfrac{1}{n_1}+\cfrac{1}{n_2}}}\sim t(n_1+n_2-2)
  1. μ1,μ2\mu_1,\mu_2未知，σ12σ22\cfrac{\sigma_1^2}{\sigma_2^2}的区间估计，枢轴量为
F=S12/S22σ12/σ22∼F(n1−1,n2−1)F=\cfrac{S_1^2/S_2^2}{\sigma_1^2/\sigma_2^2}\sim F(n_1-1,n_2-1)

总结​

image-20210113112944885

例​

image-20210115100109997 image-20210115100214582

单侧置信区间​

image-20210115100307780