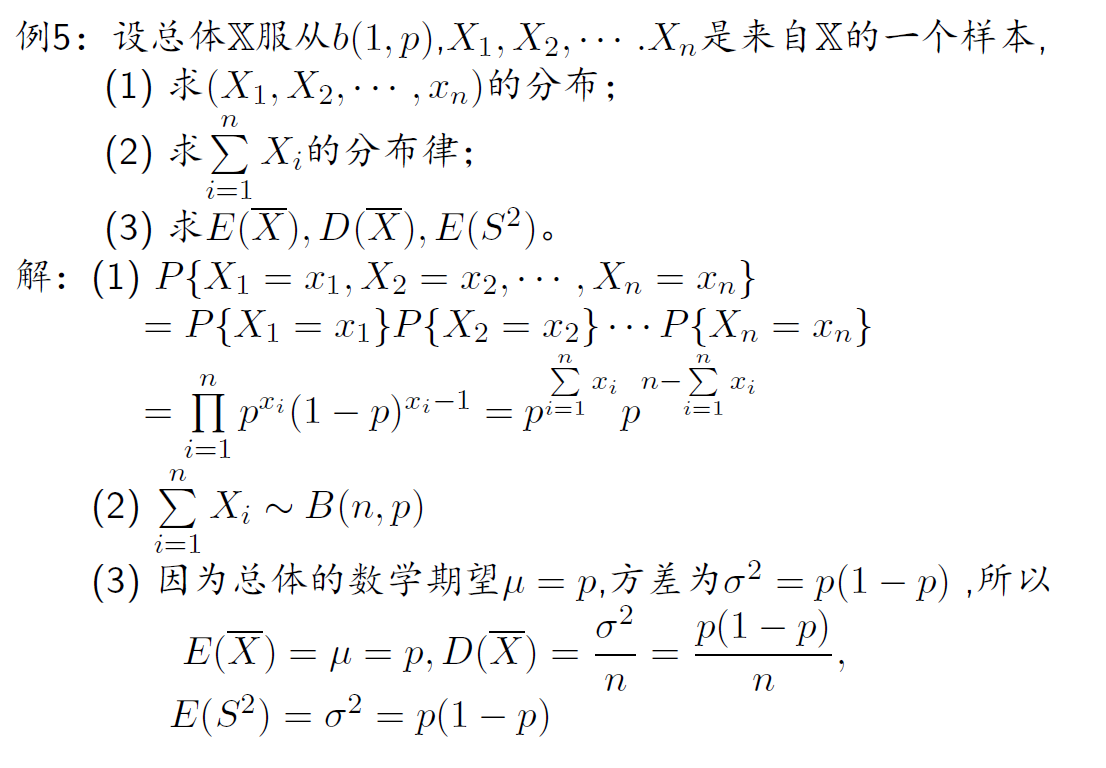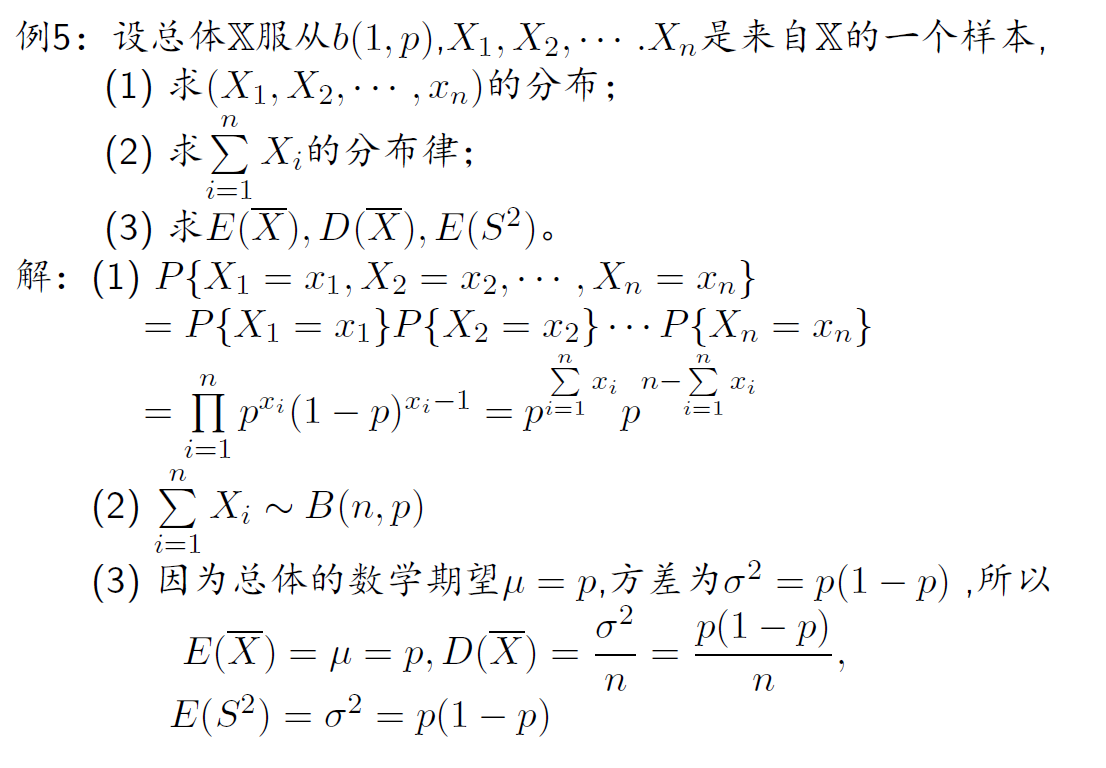样本及抽样分布
- 总体(母体):具有一定共性的研究对象的全体,记为 X
- 个体:构成总体的每一个成员
- 总体的容量:个体的个数
- 抽样:按一定的原则从X中抽取若干个体
- 样本:被抽出的部分个体(相互独立且同分布),记作X1,X2,…,Xn
- 总体分布:每一个个体可以看作一个随机变量,这个随机变量的分布即为总体分布
- 样本容量:样本是一组随机变量X1,X2,…,Xn,n即为样本容量
- 样本值:对样本进行一次观察得到的一组观察值x1,x2,…,xn
- 样本分布:样本(X1,X2,…,Xn)的概率分布,有
F(x1,x2,…,xn)=F(x1)F(x2)…F(xn)f(x)=f(x1)f(x2)…f(xn)
设 X1,X2,…,Xn 是来自总体 X 的一个样本,称此样本的任一不含总体分布未知参数的函数为该样本的统计量
统计量是随机变量,不是一个数
X=n1i=1∑nXix=n1i=1∑nxi
S2=n−11i=1∑n(Xi−X)2=n−11(i=1∑nXi2−nX2)s2=n−11i−1∑n(xi−x)2
S=n−11i=1∑n(Xi−X)2s=n−11i−1∑n(xi−x)2
Ak=n1i=1∑nXikk=1,2,…ak=n1i=1∑nxik
Bk=n1i=1∑n(Xi−X)kk=2,3,…bk=n1i=1∑n(xi−x)k
称统计量的分布为抽样分布(统计分布)
设 X1,X2,…,Xn 是来自总体 N(0,1) 的样本,则称统计量
χ2=X12+X22+…+Xn2=i=1∑nXi2
服从自由度为 n 的 χ2 分布,记作 χ2∼χ2(n)
- 性质
- χ12+χ22∼χ2(n1+n2)
- E(χ2)=nD(χ2)=2n
- 图形特征(扩展)
- 单峰曲线,在 n-2 时取到最大值
- 不对称,n 越大越对称
- 当 n 很大时可用正态分布来近似
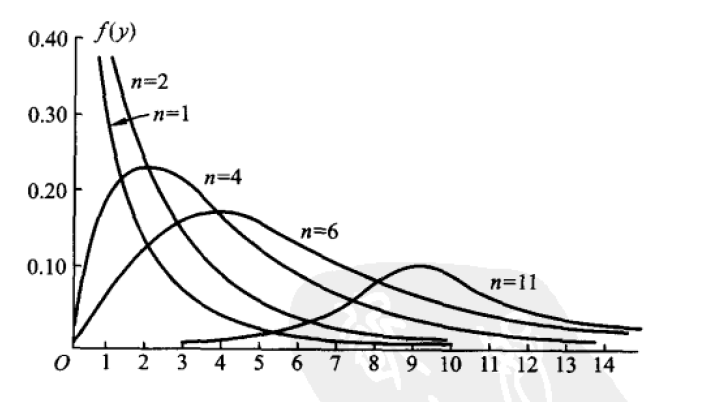
设X∼N(0,1),Y∼χ2(n),且 X,Y 相互独立,则称统计量
t=Y/nX
服从自由度为 n 的 t 分布(学生氏分布),记作 t∼t(n)
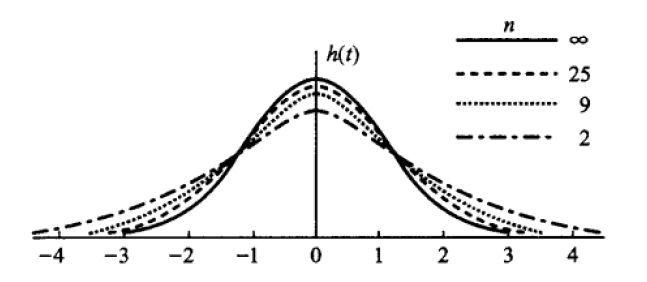
设 U∼χ2(n1),V∼χ2(n2),且 U,V 相互独立,则称统计量
F=V/n2U/n1
服从自由度为 (n1,n2)的 F 分布,记作 F∼F(n1,n2)

(Quantile)
对随机变量X,0<α<1
- 若P{X>tα}=α,则称tα为X的上α分位点
- 若P({X<tα1}∪{X>tα2})=α(α1+α2=1),则称tα1和tα2为X的双侧α分位点
通常取α2=α/2,α1=1−α/2
设 X∼N(0,1),若数 zα 满足
P{X>zα}=α,0<α<1
则称 zα 为标准正态分布的上 α 分位点

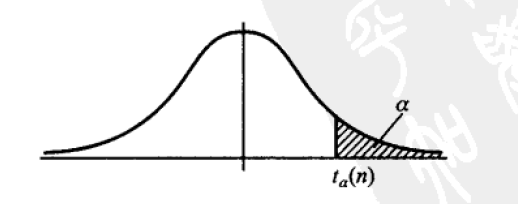
设X2∼X2(n),若数Xα2(n)满足
P{X2>Xα2(n)}=α,0<α<1
则称Xα2(n)为X2(n)分布的上α分位点
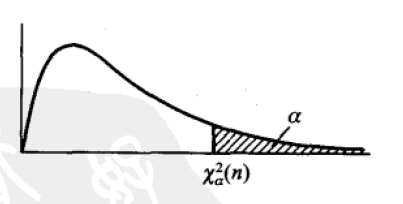
设 t∼t(n),若数 tα(n) 满足
P{t>tα(n)}=α,0<α<1
则称 tα(n) 为 t(n)分布的上 α 分位点
- 有t1−α(n)=−tα(n)
设 F∼F(n1,n2),若数 Fα(n1,n2) 满足
P{F>Fα(n1,n2)}=α,0<α<1
则称 Fα(n1,n2) 为F分布的上 α 分位点
- 有Fα(n1,n2)=F1−α(n2,n1)1

| 分布名 | 上 α 分位点 | 双侧 α 分位点 |
|---|
| 标准正态分布 | zα | ±zα/2 |
| X2 分布 | Xα2(n) | Xα/22(n)X1−α/22(n) |
| t 分布 | tα(n) | ±tα/2(n) |
| F 分布 | Fα(n1,n2) | Fα/2(n1,n2)F1−α/2(n1,n2) |
设总体X的均值为μ,方差�为σ2,X1,X2,…,Xn是来自X的一个样本,X和S2分别为该样本的样本均值和样本方差,则
E(X)=μ,D(X)=nσ2E(S2)=σ2
设总体X的分布为N(μ,σ2),X1,X2,…,Xn是来自X的一个样本,X为该样本的样本均值,则
(1)X∼N(μ,σ2/n)(2)σ/nX−μ∼N(0,1)
设总体X的分布为N(μ,σ2),X1,X2,…,Xn是来自X的一个样本,X和S2分别为该样本的样本均值和样本方差,则
(1)σ2n−1S2∼χ2(n−1)(2)X与S2相互独立

设总体X的分布为N(μ,σ2),X1,X2,…,Xn是来自X的一个样本,X和S2分别为该样本的样本均值和样本方差,则
S/nX−μ∼t(n−1)
设 X1,X2,…,Xn1 与 Y1,Y2,…,Yn2 分别是来自两个相互独立的正态总体 N(μ1,σ12) 和 N(μ2,σ22) 的样本,X 和Y 分别为这两个样本的样本均值,S12 和 S22 分别为这两个样本的样本方差,则
(1)σ12/n1+σ22/n2(X−Y)−(μ1−μ2)∼N(0,1)(2)σ12/σ22S12/S22∼F(n1−1,n2−1)(3)当σ12=σ22=σ2时,Swn11+n21(X−Y)−(μ1−μ2)∼t(n1+n2−2)其中Sw=n1+n2−2(n1−1)S12+(n2−1)S22
例