numpy

数组基础

属性

1. ndarray.ndim

   数组的轴（维度）的个数。在 Python 世界中，维度的数量被称为 rank（秩）

2. ndarray.shape

   数组的维度。这是一个整数的元组，表示每个维度中数组的大小。对于有 n 行和 m 列的矩阵，shape 将是 (n,m)。因此，shape 元组的长度就是 rank 或维度的个数 ndim。

3. ndarray.size

   数组元素的总数。这等于 shape 的元素的乘积。

4. ndarray.dtype

   一个描述数组中元素类型的对象。可以使用标准的 Python 类型创建或指定 dtype。另外 NumPy 提供它自己的类型。例 numpy.int32、numpy.int16 和 numpy.float64。

5. ndarray.itemsize

   数组中每个元素的字节大小。例如，元素为 float64 类型的数组的 itemsize 为 8（=64/8），而 complex32 类型的数组的 itemsize 为 4（=32/8）。它等于 ndarray.dtype.itemsize 。

6. ndarray.data

   该缓冲区包含数组的实际元素。通常，我们不需要使用此属性，因为我们将使用索引访问数组中的元素。

创建

概览

a = np.array([0, 1, 2, 3, 4])
b = np.array((0, 1, 2, 3, 4))
c = np.arange(5)
d = np.linspace(0, 2*np.pi, 5)

用列表和元组创建数组

使用 array 函数

a = np.array([2,3,4])
b = np.array([(1.5,2,3), (4,5,6)])

>>>
	array([2, 3, 4])

	array([[1.5, 2. , 3. ],
       		[4. , 5. , 6. ]])

数组类型可以在创建时显示指定

c = np.array([[1, 2], [3, 4]], dtype=complex)

>>>
	array([[1.+0.j, 2.+0.j],
       		[3.+0.j, 4.+0.j]])

用占位符创建数组

a = np.zeros((3, 4))
b = np.ones((2, 3, 4), dtype=np.int16)	# dtype can also be specified
c = np.empty((2, 3)) 					# uninitialized, output may vary

输出

array([[0., 0., 0., 0.],
       [0., 0., 0., 0.],
       [0., 0., 0., 0.]])

array([[[1, 1, 1, 1],
        [1, 1, 1, 1],
        [1, 1, 1, 1]],

       [[1, 1, 1, 1],
        [1, 1, 1, 1],
        [1, 1, 1, 1]]], dtype=int16)
array([[1.5, 2. , 3. ],
       [4. , 5. , 6. ]])

在一定范围内创建数组

使用 arange 函数

输入起始，终止，步长来创建数组

a = np.arange(10, 30, 5)
b = np.arange(0, 2, 0.3)  # it accepts float arguments

>>>
	array([10, 15, 20, 25])
	array([0. , 0.3, 0.6, 0.9, 1.2, 1.5, 1.8])

使用 linspace 函数

当 arange 与浮点参数一起使用时，由于有限的浮点精度，通常不可能预测所获得的元素的数量。出于这个原因，通常最好使用 linspace 函数来接收我们想要的元素数量的函数，而不是步长（step）

a = np.linspace(0, 2, 9)     # numbers from 0 to 2

>>>
	array([0.  , 0.25, 0.5 , 0.75, 1.  , 1.25, 1.5 , 1.75, 2.  ])

创建二维数组

用 .reshape() 方法

创建一个共 20 个整数、4 行 5 列的二维数组

a = np.arange(20).reshape(4, 5)

>>>
	array([[ 0,  1,  2,  3,  4],
       		[ 5,  6,  7,  8,  9],
       		[10, 11, 12, 13, 14],
       		[15, 16, 17, 18, 19]])

随机创建

使用 numpy.random.rand()

numpy.random.rand(d0, d1, …, dn)

1. rand 函数根据给定维度生成[0,1)之间的数据，包含 0，不包含 1

2. dn 表示每个维度

3. 返回值为指定维度的 array

np.random.rand(4, 2)

>>>
	array([[0.98674795, 0.13286586],
       		[0.29918216, 0.31617708],
       		[0.11613039, 0.06952587],
       		[0.854591  , 0.46243232]])

使用 numpy.random.randn()

numpy.random.randn(d0, d1, …, dn)

1. randn 函数返回一个或一组样本，具有标准正态分布。

2. dn 表格每个维度

3. 返回值为指定维度的 array

4. 没有参数时，返回单个数据

np.random.randn(2, 4)

>>>
	array([[-1.00153189,  2.24079402,  1.60828566, -0.65998837],
       		[ 1.98674251, -0.33065155,  0.48365328,  0.4008861 ]])

运算

基本运算符

1. 乘积运算符*在 NumPy 数组中按元素进行运算。矩阵乘积可以使用@运算符或dot函数或方法执行

A = np.array([[1, 1], [0, 1]])
B = np.array([[2, 0], [3, 4]])

A*B
>>>
	array([[2, 0],
       		[0, 4]])

A@B
>>>
	array([[5, 4],
	       [3, 4]])

A.dot(B)
>>>
	array([[5, 4],
	       [3, 4]])

1. 某些操作（例如+=和*=）会更直接更改被操作的矩阵数组而不会创建新矩阵数组
2. 当使用不同类型的数组进行操作时，结果数组的类型对应于更一般或更精确的数组（称为向上转换的行为）

特殊运算符

# dot, sum, min, max, cumsum
a = np.arange(10)
print(a.sum())  # >>>45
print(a.min())  # >>>0
print(a.max())  # >>>9
print(a.cumsum())  # >>>[ 0  1  3  6 10 15 21 28 36 45]

通过指定 axis（列）参数，可以沿数组的指定轴应用操作

b = np.arange(12).reshape(3, 4)
b.sum(axis=0)              # sum of each column

>>>
	array([12, 15, 18, 21])

通函数（ufunc）

数学函数合集

NumPy 提供熟悉的数学函数，例如 sin，cos 和 exp。在 NumPy 中，这些被称为“通函数”。在 NumPy 中，这些函数在数组上按元素进行运算，产生一个数组作为输出

A = np.arange(3)

np.exp(A)  # 以e为底的指数函数
>>>
	array([1.        , 2.71828183, 7.3890561 ])

np.sqrt(A)  # 开平方根
>>>
	array([0.        , 1.        , 1.41421356])

B = np.array([2., -1., 4.])
np.add(A, B)  # 相加
>>>
	array([2., 0., 6.])

x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])
# Matrix / matrix product; both produce the rank 2 array
print(x.dot(y))
print(np.dot(x, y))

>>>
	[[19 22]
	 [43 50]]

切片

一维数组

a = np.arange(10)**3

a
>>> 
	array([  0,   1,   8,  27,  64, 125, 216, 343, 512, 729], dtype=int32)

a[2]
>>> 
	8

a[2:5]
>>> 
	array([ 8, 27, 64], dtype=int32)

a[:6:2] = -1000  # from start to position 6, exclusive, set every 2nd element to -1000

a
>>> 
	array([-1000,     1, -1000,    27, -1000,   125,   216,   343,   512,
         	729], dtype=int32)

a[::-1]          # reversed a
>>>
	array([  729,   512,   343,   216,   125, -1000,    27, -1000,     1,
       		-1000], dtype=int32)

多维数组

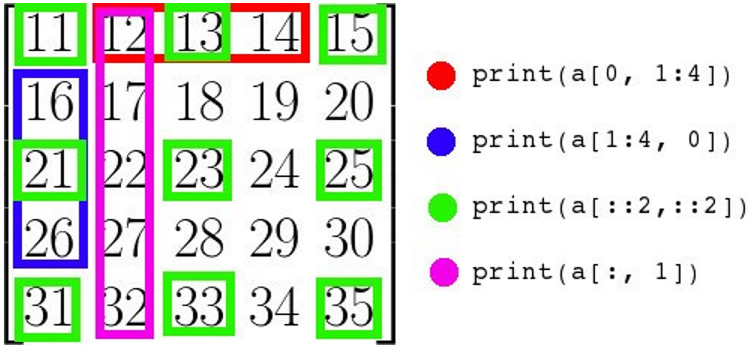
多维的数组每个轴可以有一个索引。这些索引以逗号分隔的元组给出

a = np.array([[11, 12, 13, 14, 15],
              [16, 17, 18, 19, 20],
              [21, 22, 23, 24, 25],
              [26, 27, 28, 29, 30], 
              [31, 32, 33, 34, 35]])

print(a[0, 1:4])  
>>>
	[12 13 14]
    
print(a[1:4, 0])  
>>>
	[16 21 26]
    
print(a[::2, ::2])   
>>>
	[[11 13 15]
     [21 23 25]
     [31 33 35]]
    
print(a[:, 1])  
>>>
	[12 17 22 27 32]

三个点（ ... ）表示产生完整索引元组所需的冒号。例如，如果 x 是 rank 为 5 的数组（即，它具有 5 个轴），则

x[1 , 2 , ...] 相当于 x[1,2, : , : , :]，

x[… , 3] 等效于 x[: , : , : , : ,3]

x[4, … ,5, :] 等效于 x[4, : , : , 5, : ]

调整数据

四舍五入

返回四舍五入后的值，可指定精度

np.around(a, decimals=0, out=None)

• a：输入数组

• decimals：要舍入的小数位数。 默认值为 0。 如果为负，整数将四舍五入到小数点左侧的位置

n = np.array([-0.746, 4.6, 9.4, 7.447, 10.455, 11.555])
 
np.around(n)
>>>
	[ -1.   5.   9.   7.  10.  12.]
 
np.around(n, decimals=1)
>>>
	[ -0.7   4.6   9.4   7.4  10.5  11.6]
 
np.around(n, decimals=-1)
>>>
	[ -0.   0.  10.  10.  10.  10.]

向下取整

返回不大于输入参数的最大整数

np.floor()

n = np.array([-1.7, -2.5, -0.2, 0.6, 1.2, 2.7, 11])
 
np.floor(n)
>>>
	[ -2.  -3.  -1.   0.   1.   2.  11.]

向上取整

返回输入值的上限

np.ceil()

n = np.array([-1.7, -2.5, -0.2, 0.6, 1.2, 2.7, 11])
 
np.ceil(n)
>>>
	[ -1.  -2.  -0.   1.   2.   3.  11.]

索引进阶

花式索引

用想要检索的特定索引序列对数组进行索引。这反过来返回索引的元素的列表。

# Fancy indexing
a = np.arange(0, 100, 10)
indices = [1, 5, -1]
b = a[indices]
print(a)   
>>>	
	[ 0 10 20 30 40 50 60 70 80 90]
    
print(b)  
>>>
	[10 50 90]

布尔屏蔽

Where 函数

只需要把条件传递给它，它就会返回一个使得条件为真的元素的列表。

返回索引（下标）

# Where
a = np.arange(0, 100, 10)
b = np.where(a < 50)
c = np.where(a >= 50)[0]

print(b)  
>>>
	(array([0, 1, 2, 3, 4]),)
    
print(c)  
>>>
	[5 6 7 8 9]

形状操控

改变数组的形状

a = np.array([[2,  8,  0,  6],
              [4,  5,  1,  1],
              [8,  9,  3,  6]])

可以使用各种命令更改数组的形状。请注意，以下三个命令（除 resize）都返回一个修改后的数组，但不会更改原始数组

a.ravel()  			# 展平数组
>>>
	array([2, 8, 0, 6, 4, 5, 1, 1, 8, 9, 3, 6])
    
 a.reshape(6,2)  	# 重塑数组行列
>>>
	array([[2, 8],
       [0, 6],
       [4, 5],
       [1, 1],
       [8, 9],
       [3, 6]])

a.reshape(3,-1)		# 如果在 reshape 操作中将 size 指定为-1，则会自动计算其他的 size 大小
>>>
	array([[2, 8, 0, 6],
       [4, 5, 1, 1],
       [8, 9, 3, 6]])

 a.T  				# 转置数组
>>>
	array([[2, 4, 8],
       [8, 5, 9],
       [0, 1, 3],
       [6, 1, 6]])

a.resize((2,6))		#.resize()方法会修改数组本身
print(a)
>>>
	array([[2, 8, 0, 6, 4, 5],
       [1, 1, 8, 9, 3, 6]])

堆叠数组

几个数组可以沿不同的轴堆叠在一起

a = np.array([[8,  8],
              [0,  0]])
b = np.array([[1,  8],
              [0,  4]])

np.vstack((a, b))  # 垂直(按列顺序)把数组给堆叠起来
>>>
	array([[8, 8],
       [0, 0],
       [1, 8],
       [0, 4]])
    
np.hstack((a, b))  # 水平(按列顺序)把数组给堆叠起来
>>>
	array([[8, 8, 1, 8],
       [0, 0, 0, 4]])

拆分数组

使用hsplit，可以沿数组的水平轴拆分数组，方法是指定要返回的形状相等的数组的数量，或者指定应该在其之后进行分割的列

使用vsplit沿垂直轴分割

a = np.array([[9,  5,  6,  3,  6,  8,  0,  7,  9,  7,  2,  7],
              [1,  4,  9,  2,  2,  1,  0,  6,  2,  2,  4,  0]])

np.hsplit(a,3)   # 平均分成三份
>>>
	[array([[9, 5, 6, 3],
        [1, 4, 9, 2]]),
 	 array([[6, 8, 0, 7],
        [2, 1, 0, 6]]),
 	 array([[9, 7, 2, 7],
        [2, 2, 4, 0]])]
    
np.hsplit(a,(3,4))   # 以第三列和第四列为界，分割数组
>>>
	[array([[9, 5, 6],
        [1, 4, 9]]),
 	 array([[3],
        [2]]),
 	 array([[6, 8, 0, 7, 9, 7, 2, 7],
        [2, 1, 0, 6, 2, 2, 4, 0]])]

例

1. 打印 numpy 的版本和配置说明

print(np.__version__)
np.show_config()

2. 如何找到任何一个数组的内存大小？

Z = np.zeros((10, 10))
print("%d bytes" % (Z.size * Z.itemsize))

3. 如何从一维数组中提取满足指定条件的元素？

# Input
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# Solution
arr[arr % 2 == 1]

>>>
	array([1, 3, 5, 7, 9])

4. 找到数组[1,2,0,0,4,0]中非 0 元素的位置索引

nz = np.nonzero([1, 2, 0, 0, 4, 0])
print(nz)