从零开始推导乐理

摘自乐理 101：https://zhuanlan.zhihu.com/p/24538434

快速记录

一些问题

• 为什么一四五八度是纯的？
  1. 听感上：这几个音程相对更和谐（纯四度有争议）
  2. 从转位的角度理解
     1. 大/小音程转位还是小/大音程（13 大三度，31 小六度）
     2. 纯音程转位还是纯音程（14 纯四度，41 纯五度）
     3. 增减音程转位还是增减音程（47 增四度，74 减五度）
• 纯四度和大三度哪个更和谐？（mi 和 fa 哪个更和谐？）
  • 以简单的对比角度：纯四度更和谐
  • 在以三度堆叠的和声体系下看：fa 天然趋近于 mi，在 do mi sol 大三和弦下，单独的纯四度不能提供一个稳定的解决，需要解决到大三度上去
    • 没有进行西方音乐听觉训练的人，并不会认为纯四度需要进行到三度。他们甚至不觉得三全音需要解决（比如湖北民歌）
    • 早期教会音乐也会有很多的平行四度，并不会感到不协和
  • 泛音列角度：以C的泛音列为例，F在人耳可听的前16个泛音中是不存在的。由此，纯四度在泛音列中是没有办法得到解释的
  • 历史风格：西方教会音乐很长一段时间的形态就是四度的平行进行。由此，产生了审美疲劳。所以，在后来的非教会音乐创作中就会有意识的回避。

一些技巧

• 一四五八纯增减，二三六七分大小
• 大调：全全半全全全半；小调：全半全全半全全
• 三全音=六个半音=增四度=减五度=fa -> ti
• 大调音阶之间音程计算：数数，两组半音，三组大三度，以及一对三全音
  • 数字部分的计算：数数，数多少次就是多少度
  • 两组半音：3~4，7~1
  • 三组大三度：1~3，4~6，5~7
  • 一对三全音：4~7
  • 使用转位速算音程：数字用九减，大变小，增变减，纯不变

音程的推导

我们能够从感官上分辨声音频率的倍数关系，这是音乐产生的基础。而八度就是这些倍数关系中最重要的一个，即二倍关系（从声音的频率上看，八度正好是把一个音的频率从它本身升高了一倍）

人耳除了能够体会八度之外，对有简单整数倍关系的音高频率组合会感到相对协和（三倍、五倍等），而对复杂倍数关系的音高频率组合会感到相对的不协和。物理学上，由简单倍数关系的频率组成的波，其在物体上的振动模式更为规则，而这种振动的规则性对人来讲就比较悦耳。倍数越简单就越协和，因此我们可以利用这个规则，从最小的正整数倍数开始，来挑选八度中的音程关系。

八度、五度与三度

二倍生八度，三倍生五度，五倍生三度

某个音高 Do，它频率的两倍或四倍的音还是 Do，总结一下就是 $2^{n}$ 倍的音都是 Do；所以通过八度是无法产生新的唱名的。因此，如果想要定义出新的唱名出来，我们需要探索其他的简单整数倍数来构建音程，例如三倍和五倍关系。

有一个问题：我们想要在八度的范围内来定义新的唱名和音程，但三倍、五倍音高显然已经超出了一个八度的范围。幸亏，根据八度的二倍关系，在原有整数倍数上任意地乘以或除以很多个两倍之后，依然会得到同样的唱名

也就是说，3 倍和 3/2 倍本是上是一样的，我们可以用 3/2 倍来定义这个新的音程及唱名

音乐中，我们把这个 3/2 倍的音程定义为纯五度（以下简称五度），并将 Do[1] 向上一个五度音程得到的唱名叫做 Sol[5]

基于二倍关系的纯八度是最协和稳定的音程，以至于它听上去显得过于冷硬单调。而基于三倍的纯五度音程，它的协和度仅次于纯八度，听感依旧稳定的同时，却多了一丝温度。

类似的，我们也可以用五倍关系与八度来构建另一个新的音程。

于是，我们把 5/4 倍的音程定义为大三度，将 Do[1] 向上一个大三度得到的唱名称做 Mi[3]

大三度的协和稳定性比五度又要次一些了，但是牺牲所换来的是它听起来更具有色彩感。

音乐其实是游走于协和与不协和之间的艺术，并不是越协和就越好听。协和的音程能带来稳定的体验，而不协和的音程却能为乐曲增色。对大脑来说，音乐太过稳定了就会很没劲，而太过“粗糙”不协和了则成了噪音。

就跟烧菜一样，协和的音程就是音乐里的饭菜，不协和的音程就是油盐酱醋，一般人烧菜都会放一些佐料来调味。适宜的酱料能开胃消食，但放多了容易齁住，放少又会没胃口。当然，有的人重口味一些，有的口味比较淡，每个人的音乐的品味也各不相同。在协和与不协和的两级中找到平衡是音乐能给人带来好奇和愉悦感的秘诀。

纯律

虽然大三度已经开始变得不如八度和五度那么稳定了，但是从听觉上它还是太协和了，以至于如果一个音乐只用 Do Mi Sol 来作曲的话，若没有很丰富的节奏，恐怕大家都会无聊到睡着的。所以我们需要搜寻更多的佐料，即更多特色各异的音程关系，来往音乐食材里添加。

那除了 3 倍和 5 倍之外，如果想要定义出更多的音，我们是不是可以往更高的倍数上去找呢？下一个选择就是七倍关系了。可惜的是，这个七倍音在当时的音乐家听来不是很协和，不适合邀请它加入。

那还有什么办法可以生成与 Do Mi Sol 待在一起会好听的音出来呢？我们可以就地取材，通过加加减减拼接组合这三个音程来形成新的唱名和音程。

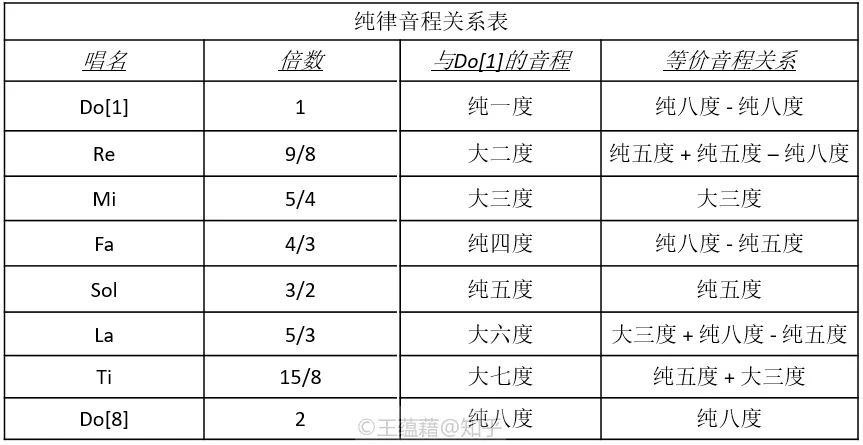
音乐家们确实这么做了。仅凭借着两倍、三倍、五倍这三个简单倍数，他们定义出了一套完整的 Do Re Mi Fa Sol La Ti 的音程关系。这个以八度，大三度，和纯五度为基础衍生出音阶上音程关系的方法被叫作 “纯律”（Just Intonation）

纯律是由弦乐上泛音列产生的律制，因其三度音与五度音这两个音程的倍数简单，它们组成的大三和弦最为纯正悦耳，故得名“纯律”。

七个唱名的设计非常科学。一方面七个音的搭配已经足以构建出丰富的音乐性，很好的平衡了音与音之间的协和与不协和性；一方面相比细分出一百个唱名来讲，七个唱名的设计保证了一般人即使没有受过训练，也可以用耳朵区分两个音的高低不同。

倍数的计算

**音程度数的加减，是音高频率在倍数上的乘除。**举例来讲：Do[1] 音高向上移动纯五度得到 Sol[5]，音高变为 Do[1] 的 3/2 倍。而 Sol[5] 向上移动纯八度得 Sol[12]，音高变为 Do[1] 的 2 × 3/2 = 3 倍。可见，纯五度叠加纯八度得到的结果是它们所对应的倍数的乘积。

其次，根据八度的定义，音程倍数任意乘除多个二倍，唱名不变。因此，倍数的分母中出现 2^n^ 是合情合理的，它可以将音程对应的频率倍数调控在 1-2 倍（一个八度）的范围内。

接下来，解释一下纯四度和大六度的分母为什么是 3 而不是 2 的倍数

• 纯四度
  • 四度是由八度减去五度产生的。八度是二倍关系，五度是 3/2 倍，2 ÷ 3/2 = 4/3；
  • 换一个角度来看，四度也是从 Sol[5] 到 Do[8] 之间的音程，算式与上面相同， 2 ÷ 3/2 = 4/3
• 大六度
  • 类似的，Do[1] 到 La[6] 之间的大六度，是由大三度加八度再减五度得到的 5/4 × 2 ÷ 3/2 = 5/3。
  • 我们已经知道，八度去掉五度是四度，所以大六度也等价于大三度叠加一个四度，5/4 × 4/3 = 5/3。
  • 甚至你也可以把它理解为是 Do[1] 的三倍音高 Sol[12] 到五倍音高 Mi[17] 之间的音程，5 除以 3 依然是 5/3 倍

最后，大二度 = 五度 + 五度 - 八度，**大七度 **= 五度 + 大三度。

综上所述，纯律中所有的音程都是由大三度、纯五度、纯八度三种音程拼接得到的。当我们明确了纯律里所有的音程倍数，我们也就继 Do Mi Sol 之后，定义了 Re Fa La Ti 各自的位置。

纯律的缺陷

然而，纯律是有缺陷的。如果我们来比较一下 Re[2] 到 Fa[4] 的音程关系的话，会发现这个音程是一个远远比其他音程复杂的倍数关系 43÷98=32/27，更糟糕的是从 Re[2] 到 La[6] 的音程 53÷98=40/27≈1.481。

而且音程不一定要从 Do[1] 向上数起，也可以从别的音算起。Re[2] 到 La[6] 之间其实和 Do[1] 到 Sol[5] 一样，是一个五度的音程。纯五度本来的音高倍数应该是 3/2=1.5 倍，现在却偏离了 1.23%。若在一个本来就不协和的音程上做微调那还好。但是，在本来极其稳定的五度上，细微的音程变化是相当明显的。这就造成以纯律定调的乐器在演奏某些音程时听上去会不协和。

纯律不只有一个，它是用小的整数倍数发展出的音律的集合。本文中特指的，用 2,3,5 三个质数作为基础的纯律叫 5-limiting tuning（以最大的质数作为名称中的数字），翻译过来就是“最大的因数为五的调律”，只是纯律中的一种。而用 2,3,5,7 四个质数作为基础的纯律就叫 7-limiting tuning。这样说来，五度相生律其实也是纯律的一个特例，用 2,3 两个质数为基础，因此也叫 3-limiting tuning。

五度相生律

这个问题早在纯律之前的五度相生律就存在了。五度相生律（Pythagorean tuning），古称三分损益律，是仅由八度和五度衍生出来的律制，所有的音程都是由二倍和三倍的数学关系组合出来的。因此和纯律不同，五度相生律中大三度的倍数是 81/64。虽然五度相生律让五度达到了最协和的音程倍数，但它的大三度相比纯律听上去可就没这么纯正了！

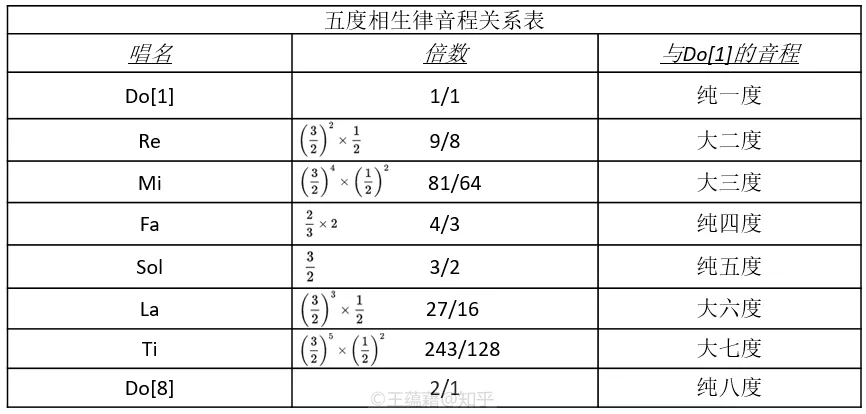
五度相生律中有一个五度并不协和，降 Re 与降 La，被称作 “狼音程“”，Wolf interval

十二平均律

那么存不存在什么办法可以让八度内的所有音程都符合简单整数倍数关系，从而变得好听呢？

答案是：不存在！我们知道 2，3，5 都是质数，而质数之间是没有整数倍的，也无法通过乘除组成新的质数。但是，确实有一种方法，可以在不满足简单整数倍的情况下，让所有的音程之间都变得好听，这个方法就叫做十二平均律（Equal temperament）

巴赫与朱载堉

人们介绍巴赫时，除了提到他是巴洛克时期的顶峰人物，一生 “多产” 之外（不光是作品多，而且他有二十个孩子），常常会带出一个音乐名词叫十二平均律。

平均律的诞生在音乐史上意义重大，它是欧洲音乐摆脱中世纪中古调式，走向现代音乐中能够随意变调的一把钥匙。你能想象在平均律之前，每一种曲调的调音都不同，乐曲想转一个调是多费周章的一项工程吗？

同样，平均律对中国人来说也是可以和四大发明一样，令国人自豪的一个创造。历史上记载十二平均律的推算者是明朝的朱载堉。不同于圆周率等其他中国早期数学发现，朱载堉在平均律的创始人地位是在世界上被公认的。

定义

十二平均律，或平均律, 是将八度的二倍音程等比例地划分为十二份的定律方式。

它让每一个临近的音在音程上都是同样的倍数关系。这每一个音和主音 Do[1] 组成的音程的倍数关系为

$$2^{n/12}, \ n=1,2,\ldots,12$$

当 n=12，倍数正好是二倍即纯八度，它对应的音名和当 n=0 时纯一度上的音是一样的。所以去掉 12，从 0 数到 11 正好产生十二个不一样的音名

虽然十二平均律是人们通过幂运算凭空创造出来的数学概念，这种律制中的音与音之间并没有正整数倍关系（除了八度），但是它的十二个音中恰好有七个音，在音高倍数关系上和纯律以及五度相生律中的 Do Re Mi Fa Sol La Ti 极为接近——以至于如果我们用十二平均律来定义音程的话，耳朵并不会明显地察觉到异样。七个音与 Do[1] 之间的音程分别近似于以下这些倍数关系：

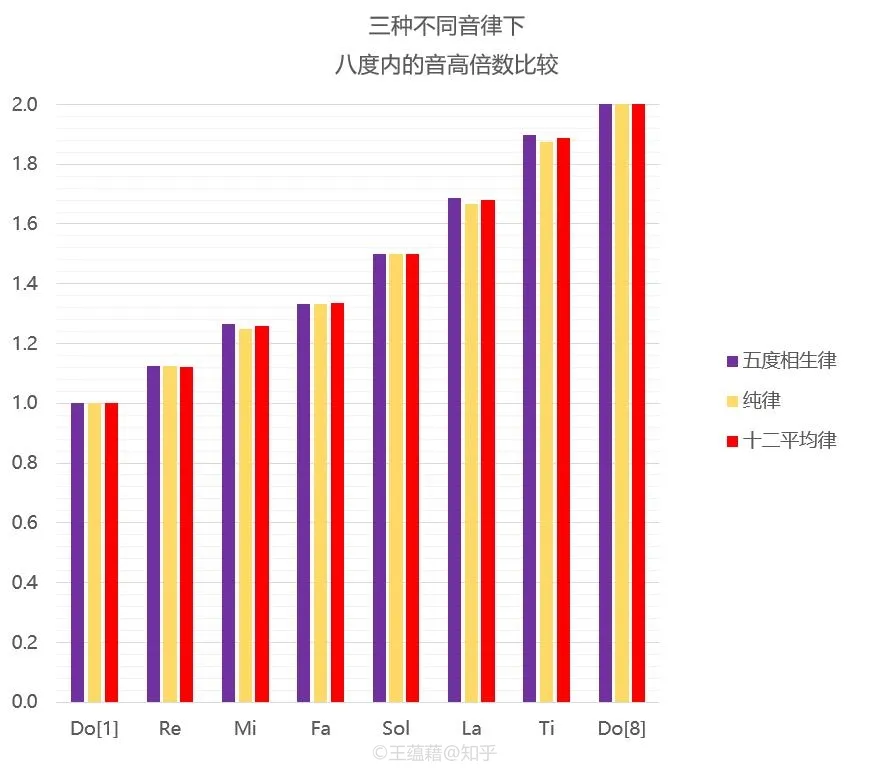
上图比较了在三种不同音律定义下，每个音在音高上的差异。我们发现十二平均律这个人工产物生成的音程竟然和五度相生律以及纯律里有自然倍数关系的音程是那么的接近，怪不得耳朵不会听着觉得古怪！（或者反过来说，我们的耳朵竟然能够自动将复杂的倍数关系约成简单的倍数关系来消化感受！）

平均律虽然轻微地牺牲了遵循简单整数倍这个让音程听着协和的自然规律，使每个音都稍稍变得不纯，但却换得了极大的好处。

• 首先，它使得**音程不再会在纯五度音程上出现不协和的问题。**平均律的纯五度倍数是 2^7/12^= 1.498，非常接近纯律中的 3/2，误差只有 0.1%。相比上一篇文章中纯律里出现过的 40/27 倍音程和 1.23% 的误差，要小了十倍。平均律中的大三度偏离纯律的程度相比五度要大，但其表现尚佳，优于五度相生律。
• 其次，平均律保证了音程倍数关系永远是固定值。
  • 比如说，从 Do[1] 到 Re[2] 之间是大二度关系，音高比例为 2^2/12^ ≈ 1.122。而 Re[2] 到 Mi[3]，以及 Fa[4] 到 Sol[5]，这两组音之间同样是大二度关系，他们的各自的比例也是 2^2/12^，倍数不会随着起始音位置发生改变。
  • 而这在纯律上是做不到的：纯律中 Re[2] 和 Mi[3] 之间的音程是 10/9 ≈ 1.111 倍的关系，与 Do[1] 到 Re[2] 的 9/8 = 1.125 倍就略有不同。
  • 不仅大二度是这样，在平均律中，任何相同的音程度数都不会随着音高的升降而改变。将调里面的所有组成音都升高或降低几度时，调内音程的倍数关系是不会更改的。
  • 因此，使用平均律的乐器可以轻松地完成转调的工作，而不需要每次为不同的调来调整音高的设置了

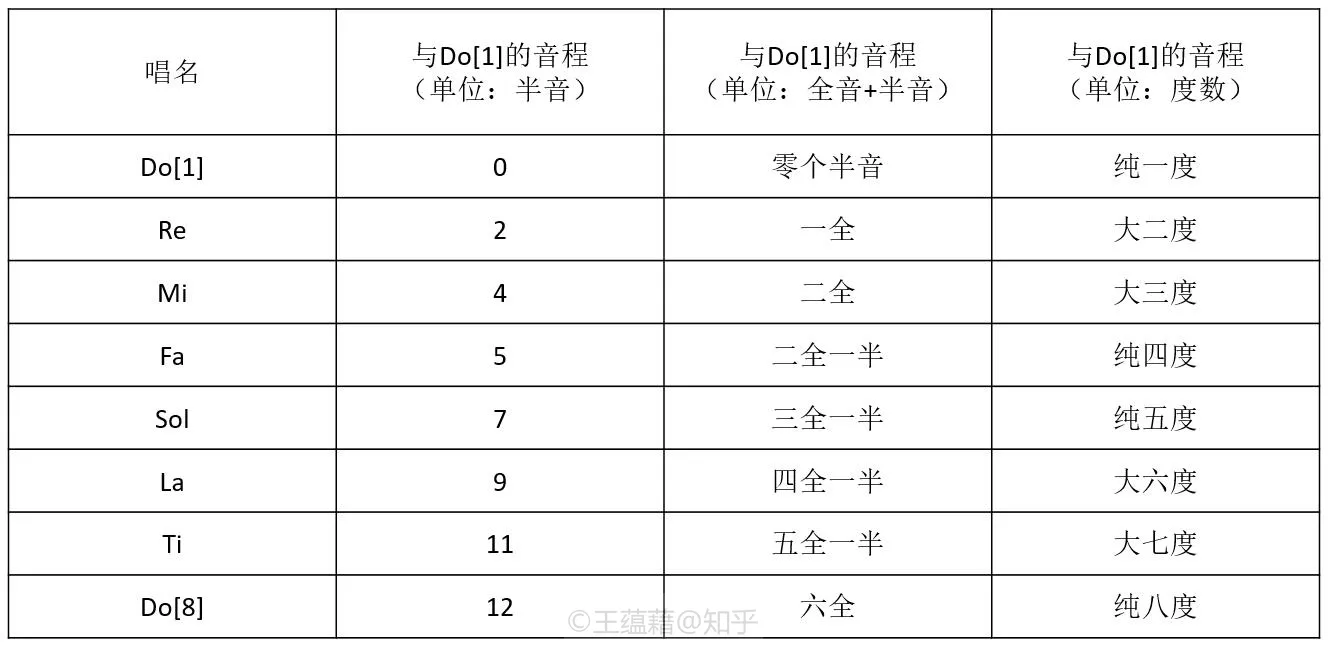
半音、全音与度数

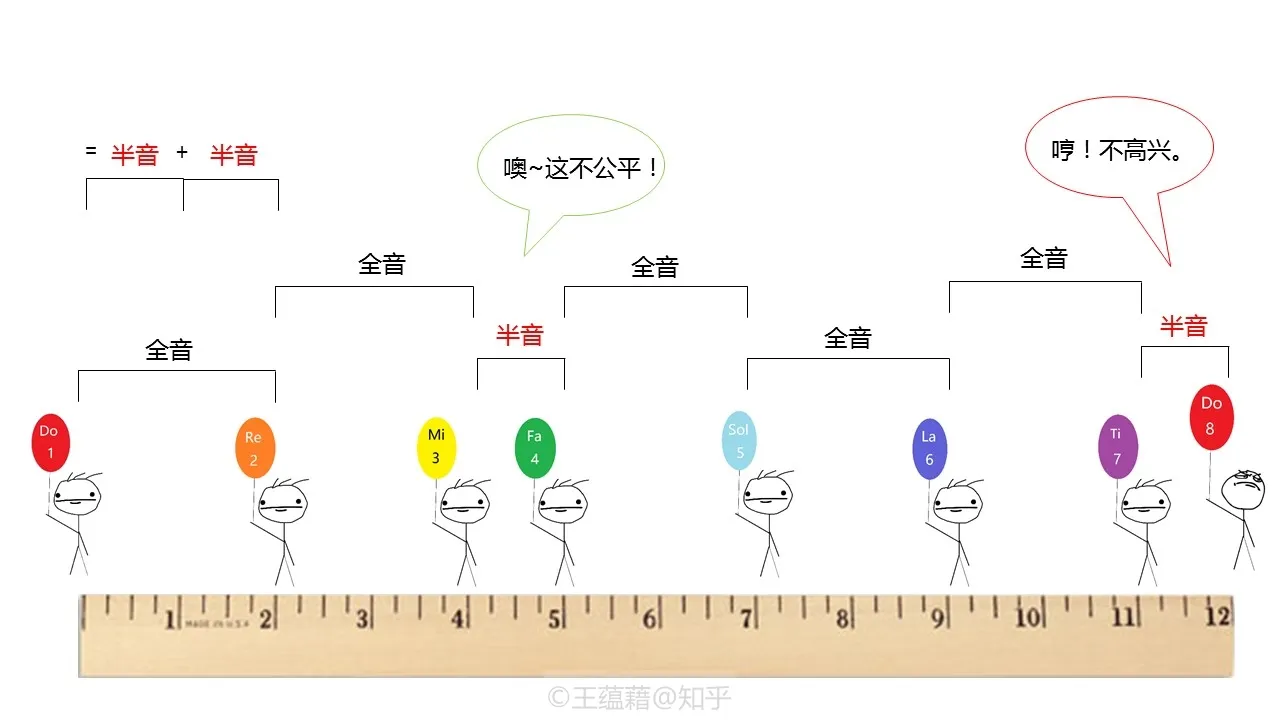
正因为十二平均律的等比关系使音阶变得“平均”，我们从此再也不需要用倍数去演算音程了，而是改为直接用整数刻度来衡量音程的“距离”

我们把平均律的十二个音中，相邻的两个音之间的音程距离（2^1/12^ 倍）叫做半音程，简称半音。半音是现代音乐中衡量音程的最小刻度。就好像一把尺子上的刻度一样，一个半音就像是 1cm 这个刻度，而一个八度的距离是 12 个刻度也就是 12 个半音。因此，我们可以重新定义八度，八度就是相差十二个半音的音之间的音程。同样，五度的定义就是七个半音程。以此类推。从此，我们在音乐上只需要用小学数学的加减法，就能解释一切乐理了！

给理工科人的解释：我们通过把音程倍数取 log2，将音高频率间的指数关系转化成了线性关系

比半音大一点的单位叫全音程或全音，全音是由两个半音程叠加组成的，等价于大二度。

可以发现，Do[1] Re Mi Fa Sol La Ti Do[8] 相邻两个音之间音程只有两种关系，一种是全音，一种是半音。Mi[3] Fa[4] 之间以及 Ti[7] Do[8] 之间都是半音，而剩下相邻音之间则都是全音。（请务必牢记这个规律！）因此，有些情况用全音与半音一起描述音程比直接用半音来得更便捷。

另外一种讨论音程的单位是度，度用来描述比半音和全音要大的音程时更加方便。纯五度，大三度，这些都是度数。如果说半音是 “厘米” 的话，全音的作用就有点像大一些的 “分米”，那度数就相当于 “米” 了。当然在一些特色的音乐中存在 “毫米” 的概念，这样的音乐叫 “微分音音乐”。

在八度的十二个音中，我们只定义了 Do Re Mi Fa Sol La Ti 七个音，剩下还有五个音是什么呢？

自然音阶

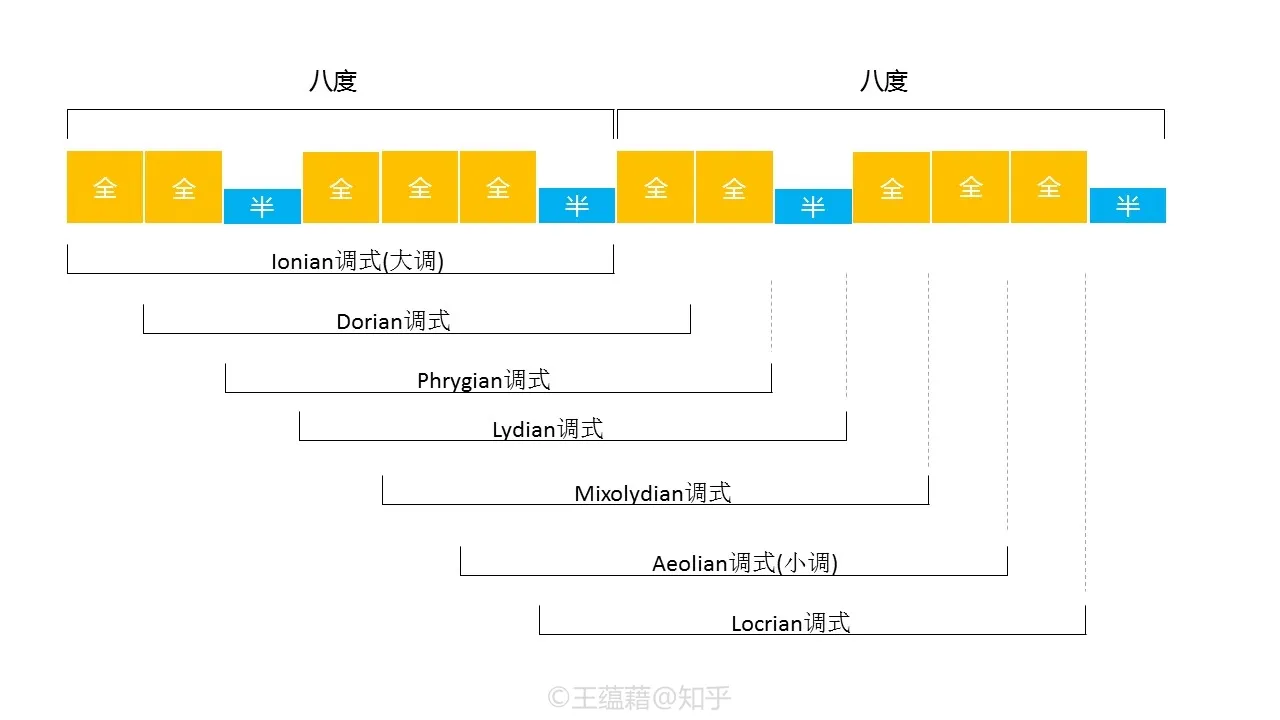
早在平均律诞生之前，由 Do Re Mi Fa Sol La Ti 七个音形成的七声音阶就在欧洲的教会音乐中普及开来。由全音，全音，半音，全音，全音，全音，半音构成的这一组音程关系我们把它叫做自然音阶，是在西方古典与流行乐中最为常见的音阶。

自然音阶一共有七种调式，从自然音阶的七个音中任何的一个音算起都能发展出一种新的调式音阶。比如从 Re 开始往上数到高八度的 Re，Re Mi Fa Sol La Ti Do Re，会产生一个 “全半全全全半全” 的音程关系，这条音阶排列叫做 Dorian 调式音阶。

随着时代的更迭，在自然音阶的七种调式中，渐渐有两种调式在使用中占了上风，成了最常用的调式。

• 第一种叫 Ionian 调式，以 Do 为主音，音阶向上以 全全半全全全半 排列，构成 Do Re Mi Fa Sol La Ti，它后来就被大家起了一个绰号叫做 “大调”（现在知道为什么 Do 是第一个唱名了吧）
• 而第二种 Aeolian 调式，以 La 为主音，音阶向上以 全半全全半全全 排列，构成 La Ti Do Re Mi Fa Sol，后来就被叫做“小调”

平均律中的唱名与音程

现在说回十二平均律。十二平均律中的十二音本来应该众生平等，和 Do Re Mi Fa Sol La Ti 一样，拥有自己独立的唱名。

然而，大调在音乐中的地位是如此不可动摇，在起名时竟也对大调中的唱名有所偏袒。

• 这是因为基于大调的唱名在公元 1000 年左右就由圭多达莱佐发明了，一开始只有前六个音，唱法也和现在不一样，后来加入了 Ti，变成现在这个样子。
• 而朱载堉的十二平均律则要到 1584 年（明万历十二年）才被提出来，欧洲亦是在十六世纪才开始对十二平均律的探索，比唱名的诞生晚了好久

⭐ 因此十二平均律中的非大调音只能和大调共享已有的唱名了。于是无奈的，出现了以下的命名法则：

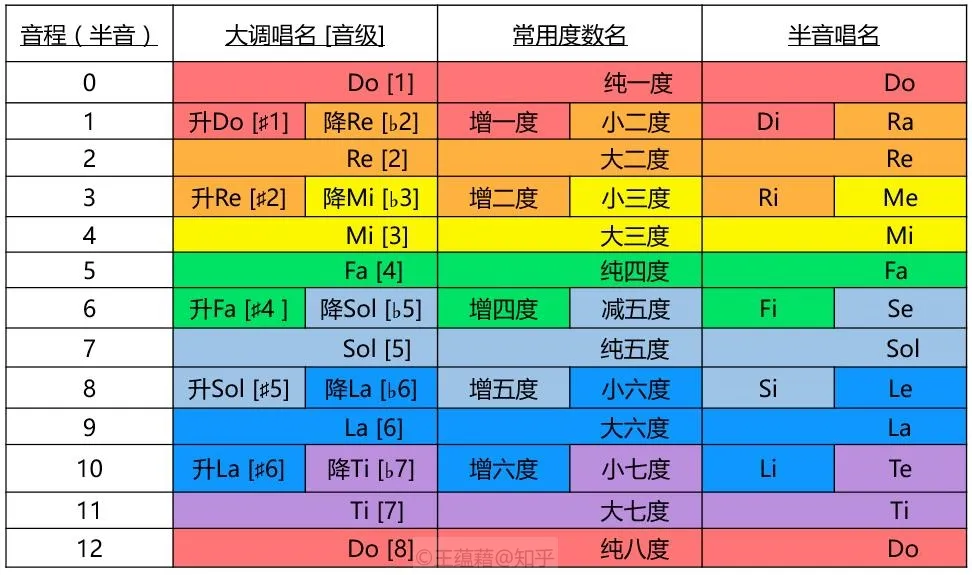
大调唱名和音级

首先，根据大调音阶，我们可以分别给 Do Re Mi Fa Sol La Ti 标上对应的数字 1-7，高一个八度的七音则为 8-14，这个数字叫做大调的音级或级数。

音级与唱名两相对应，当我们看到数字 5 时，心里面会想到 “Sol”，Sol 是大调的 5 级音。而看到 9 时就会想到 “高八度 Re”，想到高八度 Re 就知道是大调的 9 级音。由于大调音级数字与唱名是互相照应的，而且数字要比用唱名写起来更方便，我们接下来可以直接用大调的音级取代唱名来分析音乐。

小学课本里的简谱其实也是在用音级替代唱名。有所不同的是，简谱中只用到数字 1-7 代表大调的音，数字 0 代表休止不发声音。遇到升降八度时，简谱分别是在数字上方或下方加一个点来标明。

变化音和变音符号

接着，介绍一下唱名的变化音和变音符号。它们的定义和例子如下：

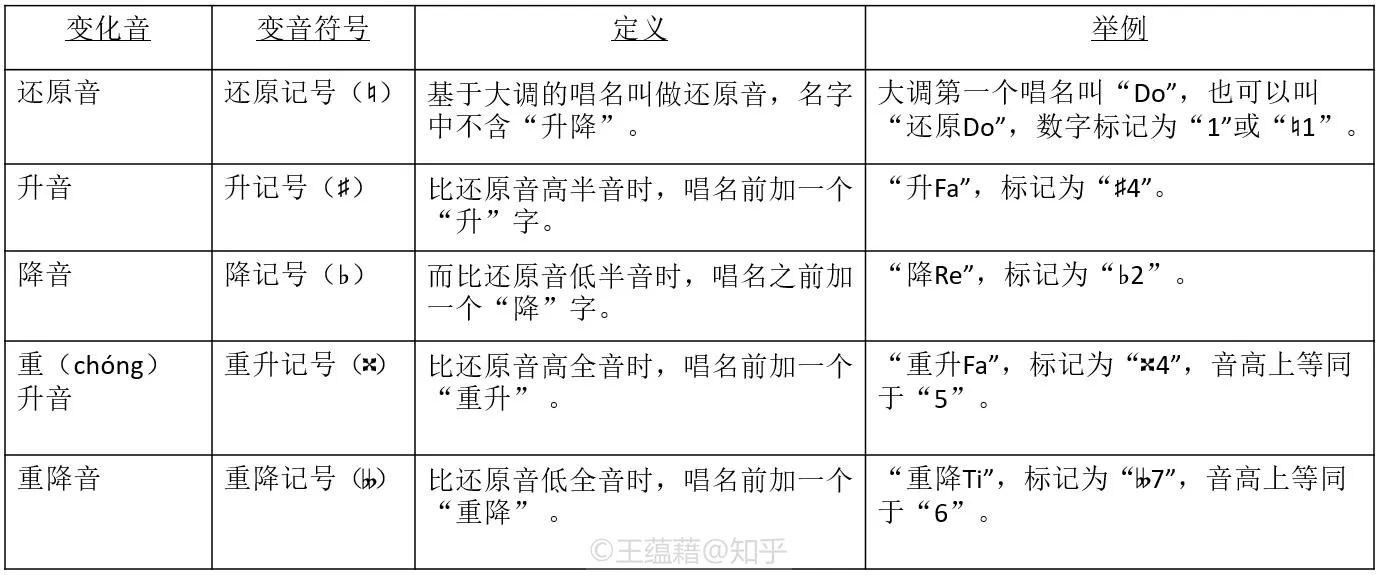
大调中未经变化的七个音 1 2 3 4 5 6 7 我们定义为还原音（或本位音、自然音），平均律中剩下五个非还原音都叫作变化音。

• 还原音在音级数字不变的情况下，往上升一个半音叫升音，用 ♯ 号表示，念 “升记号”。
• 还原音降半音得到降音，用♭号表示，念 “降记号”。
• 还原音如果升或降一个全音，叫重升音和重降音，“重” 字发音同 “重复”。

由于十二平均律里面半音的音程均等，比 1 高半音又比 2 低半音的这个音既可以叫 “#1” 也可以叫 “b2”，他们虽然音级和功能不同，但是在音高上是相同的音，对于演奏者来说在同一个键位

大调其他四个调外音也是如此。根据变化音符的定义，平均律中的十二个音的每个音可以同时有很多不同的名字，比如说 4 = ♮4 = #3 = bb5，或者 7 = b8 = x6，但最常用的记法还是像表格里面的一样。

唯一有一个例外：因为 1 对应着零个半音，再降就变负的了，在音乐上我们不希望出现 “往上升 -1 个半音” 这种诡异的沟通方式，因此 1 是没有降音和重降音的。当然，8 是可以有降音和重降音的。

音程度数

音程度数的命名也和大调结构息息相关。

以 Do[1] 为起点出发向上，到达大调中任何一个距离 Do[1] 不超过八度的音，其所构成的音程中，最为协和稳定的音程被称为纯音程，这包括了一、四、五和八度。而其余的音程都称为大音程，包括二三六七。

除了大调内的七个音，大调之外还有五个音。以 Do[1] 为起点出发向上，到达这五个调外音所构成的音程中，除一个例外，剩下的四个音程都可以用小音程命名：1 个半音为小二度，3 个半音为小三度，8 个半音为小六度，10 个半音为小七度。

这唯一的一个例外是由 6 个半音（3 个全音）构成的音程。它既不是纯音程，也不是大音程或小音程，而是一个减五度或增四度音程。下面我们来看为什么这么命名。

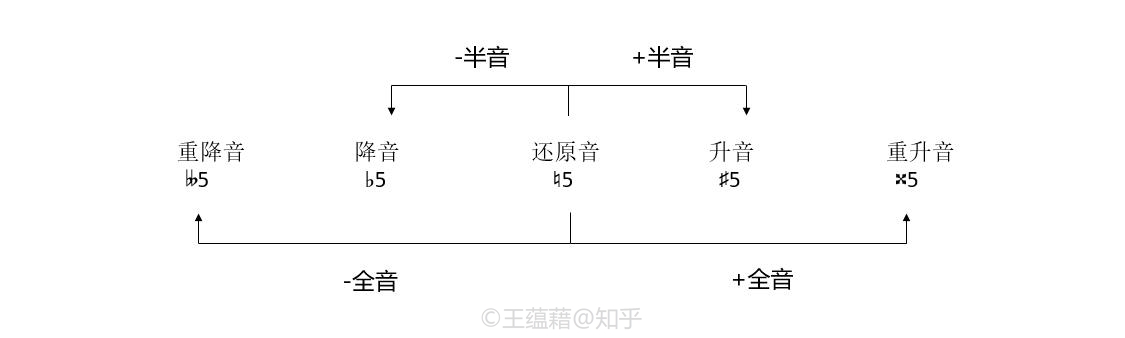
同唱名有升降变化一样，音程也有不同的属性，如下图所示：

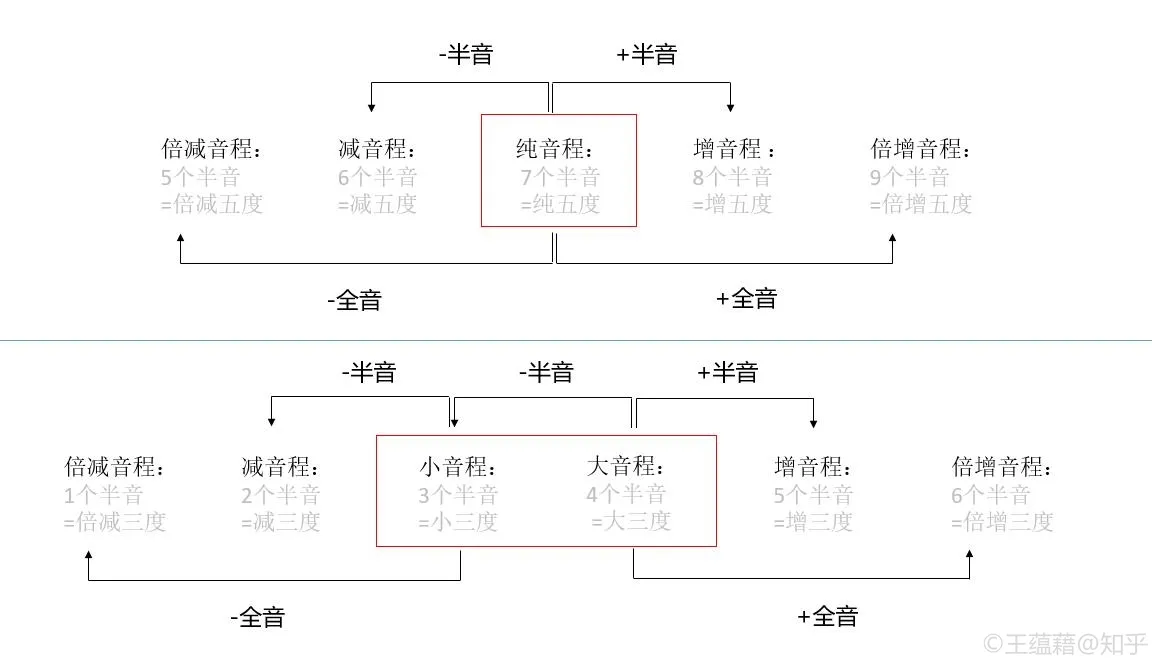
大音程减半音得小音程。小音程减半音得减音程，再减半音得倍减音程。大音程加半音得增音程，再加半音得倍增音程。而纯音程就像一个大胖子，一个人占了大小音程的位置，加减半音直接得到增减音程。这就解释了为什么纯五度下方音程为减五度，而不存在“小五度”这种错误的说法（既然是“纯”的，那就不分“大小”了嘛）

在音乐实践中，纯音程和大小音程的出现频率是最高的，增减音程远远次之，而倍增与倍减音程则极少会出现。对于像三度这样将音程度数区分为大与小的命名模式，其意味着着大三度与小三度在音乐中出现的比重相当。而像五度这样以纯音程命名情况，则意味着纯五度几乎占据了在五度上的唯一主导地位。因此，这样的命名并不是空穴来风。我们后续会看到，它将有效帮助我们深入理解大小调。

唱名和音程是彼此挂钩的。比如描述从 1 到 b3 的音程时我们使用 “小三度”，而当描述从 1 到 #2 的音程时我们使用“增二度”。虽然两个音程大小相同都是三个半音，但是由于一个是三度一个是二度，在调式中功能会有所不同，所以不能混淆着使用。

虽然彼此挂钩，但是唱名的升降和音程的增减却并不完全对应。由于自然音程中存在“纯”和“大小”这两类互相独立的音程命名模式，导致会出现以下情况：比如同样是“减”音程，从 1 到 bb3 是减三度，有两个降号（一个重降符号）；而从 1 到 b5 是减五度，却只有一个降号。在自己推算音程与唱名音级时要格外小心。

半音唱名

如果我们启用大调唱名系统来唱歌，会遇到一个很尴尬的事情，就是如果一个旋律恰好是 1 b7 b6 b5 b4 b3 b2 1，我们难道要跟着唱：“Do 降 Ti 降 La 降 Sol 降 Fa 降 Mi 降 Re Do”？这么多降号，唱起来多费力啊！那我们不唱升降号可不可以？可以，但是万一一条旋律是 1 2 b3 3 5 1，不唱升降号就没法区分 b3 和 3 了。这对于现代大量的无调性音乐，动不动十二个音都用的曲子来说，简直是一场噩梦。

为了简化平均律上十二个音的唱名，大约上世纪初，出现了一套每个唱名都只有一个音节的系统叫做半音唱名法，与上文介绍的大调唱名法有所不同。我们从 Do Re Mi Fa Sol La Ti 中抽取出 D R M F S L T 七个辅音

• 比还原音高半音时（升音），在辅音后加上元音 i；
• 在比还原音低半音时（降音），在辅音后面加上元音 e（Re 还原音本身就跟着 e，所以降 Re 改叫 Ra）

比如升 Fa 可以改写为由 F 和 i 组合出 “Fi” 这个唱名，降 Mi 则可以改写为由 M 和 e 组成的 “Me”。根据这个规则，我们就得到了第一张表中的所有半音唱名。这套唱名用于爵士这类变化音多的音乐就非常的合适。

升 Sol 可以改写为 Si。而 Si 在国内音乐教材中指的是大调的七级音，会产生避免混淆。这就是为什么我们要把七级音叫成 Ti

流水的唱名

所有的唱名都是以 Do 作为参照物定义出来的。只要把任何一个音高设定为 Do，其他所有唱名的音高就可以通过音程推算出来。

• 比如 Do 如果是 100Hz，那 Mi 就是 100 × 2^4/12^ = 126Hz，而 Sol 就是 100 × 2^7/12^ = 150Hz。
• 如果 Do 改为 200Hz，那 Mi 就变成了 252Hz，而 Sol 就变成了 300Hz。
• 所有的音都升高了一倍，但他们之间的音程比例关系是固定不变的。

虽然唱名和 Do 之间有固定的音程，但 Do 本身的音高却是可以任意挑选的，不受任何音程关系的约束。因此，唱名系统是一个音高可以平移的体系。在与主音 Do 保持固定音程的条件下，所有唱名的音高都可以跟随 Do 一同平移任意个半音。

铁打的音名

在独自一人唱歌时，唱名体系很好用。每个人都可以根据自己的嗓音设定 Do 的音高。但是一旦有多个乐器或人声一同发声时，唱名体系就遇上困难了。如果每个人的 Do 都不一样，我的 Do 是我打哈欠时候的音高，你的 Do 是微波炉热饭时候的音高，他的 Do 是婴儿向大人发出科学 の 超音量砲伤害效果拔群时的音高，那大家就不能愉快玩耍了。

所以，在大家讨论音乐时需要为音高命名。音高的名字就叫做音名。在平均律中，每个八度都有十二个音。这些音可以用七个英文字母 ABCDEFG 配以变音记号来表示。我们将 440Hz（精确到整数）定义为所有音名的参照点，叫做“标准音高”。标准音高上的音名是 A，因此也被叫做 “A440”

A 升高一个全音得到 B，而 A 升高一个半音得“升 A”或“降 B”，标记为“A♯”或“B♭”（注意：音名的变音记号写在字母的后面，而唱名的变音记号写在数字的前面）。同唱名一样，带有升降等变音记号的音叫做变化音，而不带记号的七个音叫做还原音。

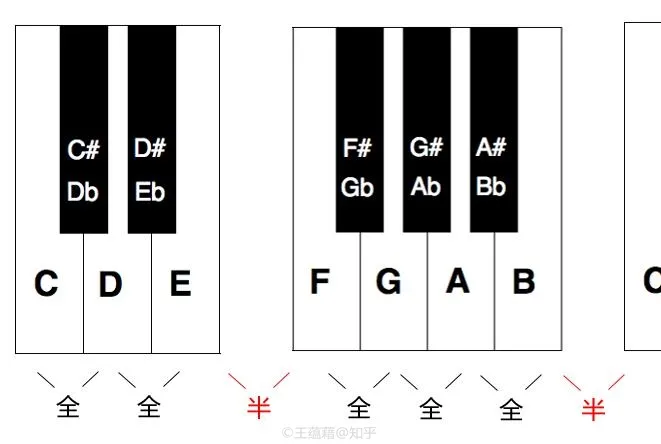
从音高 A 向上数一个八度，ABCDEFGA 这些还原音会组成一个 全半全全半全全 的音阶，这正好是我们上一讲中提到的自然音阶中 Aeolian 调式，即小调的音阶。

而如果从 C 开始音高向上数一个八度，CDEFGABC，所有还原音则会组成 全全半全全全半 的音阶，恰恰是 Ionian 调式，即大调的音阶。

由于大调的广泛应用，我们常常会把 C 默认为八度中的第一个音。同之前把 Do 看做是唱名的第一个音一样，这只是出于方便实用的考量，并非必须。在标准音高下方的第一个 C 叫做 “中央 C”，频率约为 261.6Hz。标准音高就落在中央 C 和高音 C 的八度中间。

由于 CDEFGABC 和 Do Re Mi Fa Sol La Ti 都组成大调音阶，因此当我们把主音 Do[1] 设定在 C 音时，Re 就落在 D 上面，Mi 对应 E，Fa 对应 F，Sol 对应 G，La 对应 A，Ti 对应 B，Do[8] 对应 C，七个唱名中的还原音都正好落在了七个还原音名上面。

以 C 为 Do 的大调就叫做 “C 大调”，C 大调中的 7 个音正好是 CDEFGAB。在所有的大调中，只有 C 大调中所有音高都是还原音。换一个例子，如果以 G 作为大调主音 Do，那么 Do Re Mi Fa Sol La Ti 则分别是 G A B C D E F# ，音高中就出现了一个升音记号。

音阶与调式

八度中选取任意一组音，它们的音高由低到高依次排列就能组成一条音阶。

音阶就像是楼梯，其中每个音都比它前面的那个音要高出一个台阶。每级台阶的高度不一定均匀，不同音阶的 “形状” 也因此各不相同。

• 比如大调音阶的音程组合是：全全半全全全半，在全音程组合中掺杂着两个半音程；
• 而小调则是全半全全半全全，与大调音阶形状就有所不同。

音阶不需要包括所有十二个音，它可以只包含八个音，三个音，甚至只有一个音也叫音阶。像大调这类有七个独立的音的调式音阶就叫做七声音阶。

音阶中最稳定的一个音叫做主音。以主音为第一级，音阶中每节台阶都有自己的编号，叫作音级。音级体现了每个音与主音之间的关系，它也可以用来衡量音与音之间的音程距离。

在大调中，主音 Do 的音级数字是 1，Re 的音级是 2，Mi 是 3，以此类推。而平均律中，非大调音阶的音级可以在数字前标记升降号来表示，比如降 Mi 是 b3。

音阶的类型叫做调式（mode）。从主音出发，特定的音程组合形成特定的调式类型，如大调，小调，或下文会介绍的 Dorian 等。每一类调式都具有固定的音阶 “形状”，“台阶数量”，以及独特的听觉色彩。调式的名称是由主音的音名搭配调式类型构成的，比如 C Ionian 或 D Dorian。

调、调性、以及西方音乐体系

调性音乐

公元 1600-1900 年在西方音乐史上被称为 “共性写作时期”，时间贯穿巴洛克，古典主义，浪漫主义三个重要音乐时期。

一般大众对古典音乐的理解都来源于共性写作时期的作品。在共性写作时期的的作品中，大调与小调两种调式类型确立了垄断地位。古典音乐家们在实践过程中经过总结，建立出了以大调与小调为模板框架的西方传统音乐体系——调性音乐（Tonal Music）。现代流行乐也普遍建立在调性音乐之上。

由 12 个不同的主音音名搭配大调或小调调式可以形成的调性音乐中的 24 种的基础写作模板框架，称之为 “调”（key）。在某一个调上的乐曲，它所用到的音将主要来自于这个调的音阶。比如以 C 大调来定调的作品，主要是以 C 大调音阶 CDEFGAB 这七个音作为基础创作的。而十二平均律中的另外五个音出现的频率则低很多，作品中偶尔会穿插这些调外音以起到特定的过渡或惊喜作用。

“调” 的命名方式同调式一样，由主音音名与调式类型构成，如 C 大调或 a 小调。调名中所说的调式类型特指大调或小调。一般习惯上，大调的调名中的英文字母为大写，而小调调名中的英文字母为小写。调名中如果没有标明“大”或“小”，则默认为大调，如 “G 调” 等同于 “G 大调”。

“调性” (tonality) 这个词具有多重意思。当我们说一首音乐作品具有调性的时候，往往意思是说这个作品具有明确的主音位置，根据主音的位置，我们可以听出调中每一个音的功能以及它们与主音的位置关系。

不过，有调性的音乐与“调性音乐”的意思并不相同。

• “调性音乐”特指共性写作时期所使用的基于大小调组织起来的音乐体系。
• 除了调性音乐体系，调式音乐（modal music）也是具有调性的。调式音乐使用的是非大小调的调式音阶，它也可以通过有规律地组织音高与和声形成明确的主音位置。
• 但由于调式音乐不具备大小调特有的和声功能，写作模式上与调性音乐不一样。因此调式音乐与调性音乐，虽然都具有调性，但是在概念上是两个概念。

无调性音乐

到了十九世纪末，传统的调性音乐已经被挖掘到了极致，大量调外音的使用使得调性发生松动。现代音乐家为了拓展音乐的可能性，甚至开始通过专业技巧故意使主音位置听感上难以分辨，从而彻底模糊了乐曲的调性——这类音乐体系叫做无调性音乐（atonal music）

日常用语中，“调性”常常和“调”发生混淆，会被用来讨论调的主音位置，或是区分这个调是大调还是小调。“调性”偶尔也被用来描述调式的听感 ，如 “Dorian 调式的调性”。此时这个词的适用范围就超出调性音乐的范畴，不仅限于大小调了。

自然音阶与它的调式小伙伴们

还记得上次记忆钢琴键盘的方便法门吗？八度内琴键可以分成两个区块来记忆。现在注意一下两个区块的白键，小的区块的三个白键构成两个连续的全音程，而大的区块四个白键构成三个连续的全音程， 而两个区块边缘的白键是由半音程连接的。

像钢琴键盘白键这样，一个双全音群和一个三个全音的群，两个群由半音衔接在一起，这样组成的音阶就叫做自然音阶。自然音阶有七个不同的音，因此属于七声音阶。由于八度的循环性，自然音阶中的任意一个音作为主音向上数都能发展出一种新的调式音阶。

自然音阶七种调式各自拥有独特的气质。其中两种调式是现代音乐最常用的。

• 第一种叫 Ionian 调式，音阶的音程向上以 全全半全全全半 排列，我们在调性音乐中称它为“大调”。
  • 大调的七个音级是 1 2 3 4 5 6 7。大调音乐我们从小一直在听，最为习惯。用大调写的音乐一般给人的感觉或轻松舒缓或积极阳光。
  • 大调是自然音阶的一级调式，或者叫“调一”。在日常交流中，“自然音阶”和“大调”往往指的是同一个意思，常常混着使用。
• 第二种 Aeolian 调式，音程向上以 全半全全半全全 排列，调性音乐中称“小调”。
  • 小调的七个音级是 1 2 b3 4 5 b6 b7。小调音乐带有忧郁哀伤的气质，与大调的阳光产生鲜明的对比，这个不同主要来自于三度音的大小差异。

对于初学者，大调与小调是最值得掌握的两种调式，应该试着做到熟记大小调的各个音级和音程，明确两者的区别，并能够感知大小调歌曲不同的情感色彩。

接下来要介绍的自然音阶的其他调式，初学者可以暂时忽略，建议等对大小调有了足够的理解和乐器演奏或声乐基础后再开始记忆和学习。

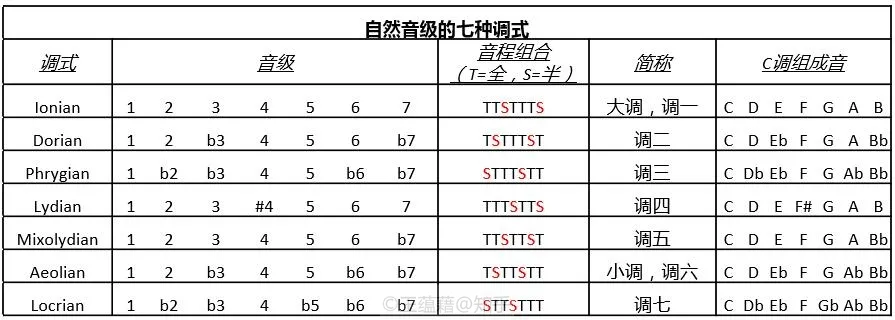
实用性上，重要程度仅次于前两者的是 Mixolydian 和 Dorian 调式。将来我们有机会会介绍，它们分别是属七和弦与小七和弦的对应音阶。两个调式听觉色彩上介于大调的阳光和小调的阴郁之间，在爵士，蓝调，先锋摇滚的曲目中不可或缺。

其次是 Lydian 和 Phrygian 调式。

• Phrygian 的二级音是降音，比小调还幽暗冷酷，由于声音色彩张力丰富，弹重金属的人很喜欢用。
  • 而西班牙或阿拉伯音乐中将 Phrygian 的三级 b3 改为还原音 3 产生 Phrygian Dominant 调式，极有异域风情。
• Lydian 则是一个具有神秘感和夸张戏剧性效果的音阶，可以在电影配乐中既可以用来烘托雄伟隆重的气氛，又可以用来渲染滑稽的情节。

最后，Locrian 黑暗气质最重，给人沉重压抑堕落的死亡气息，音乐风格的限定比较大，流行乐中最少见，用在恐怖片里倒是很合适。

在记忆调式名称时，可以注意所有英文名称的后缀都是 -ian，而每种调式名称的开头第一个字母都是不一样的，所以可以用首字母来方便记忆。

感受不同调式的性格特征：https://zhuanlan.zhihu.com/p/24890979

关系调（式）与同主音调（式）

自然音阶的调式之间是存在关联的。由 C 大调（CDEFGAB）的二级音开始数一个八度就能得到 D Dorian 调式（DEFGABC），形成 全半全全全半全 的音程组合。C 大调和 D Dorian 调式的七个音是一样的，只是主音的位置发生了改变。像这样由同一条音阶形成的共享所有音名的两个调式就叫做关系调式。

在调性音乐中，由同一条音阶形成的大小调互称为关系调，或关系大小调。

• 把大调的六级音作为主音重新构建音阶就可以得到这个大调的关系小调
• 把小调的三级音（b3）作为主音重新构建音阶就可以得到小调的关系大调

比如 C 大调（CDEFGAB）和 a 小调（ABCDEFG），或者 G 大调（GABCDEF#）和 e 小调（E F# GABCD）。对于初学者，最值得牢记的关系调式就是关系大小调了。

由于主音不同，关系大小调所表达的性格情绪完全不同，不能视为同一种调。

简谱往往把小调音级 1 2 b3 4 5 b6 b7 用关系大调的音级标注 6 7 1 2 3 4 5。

• 这样做的好处是唱起来方便，不带升降号，唱的出大调就唱的出小调。
• 但是坏处也很明显，就是没有区分出调性，明明是 a 小调，主音的标注却是 “1=C”。
• 这样做需要分析歌曲后才能判断是大调还是小调，而且没法直观的看出小调的音级。使用简谱的读者需要学会通过聆听歌曲的情绪色彩，以及关注简谱上的细节来判断大小调，比如说歌曲是以 1 结尾还是以 6 结尾，和弦的进行更像大调还是小调。

而用同一个音名作为主音的调（式）之间互为同主音调（式）。比如 C Mixolydian （C D E F G A Bb）与 C Dorian （C D Eb F G A Bb）就是同主音调式，他们之间并不共享所有音名，只要求主音相同。

知道关系调（式）与同主音调（式）的概念对我们将来理解歌曲的转调会很有帮助。

五声音阶与中国传统音乐

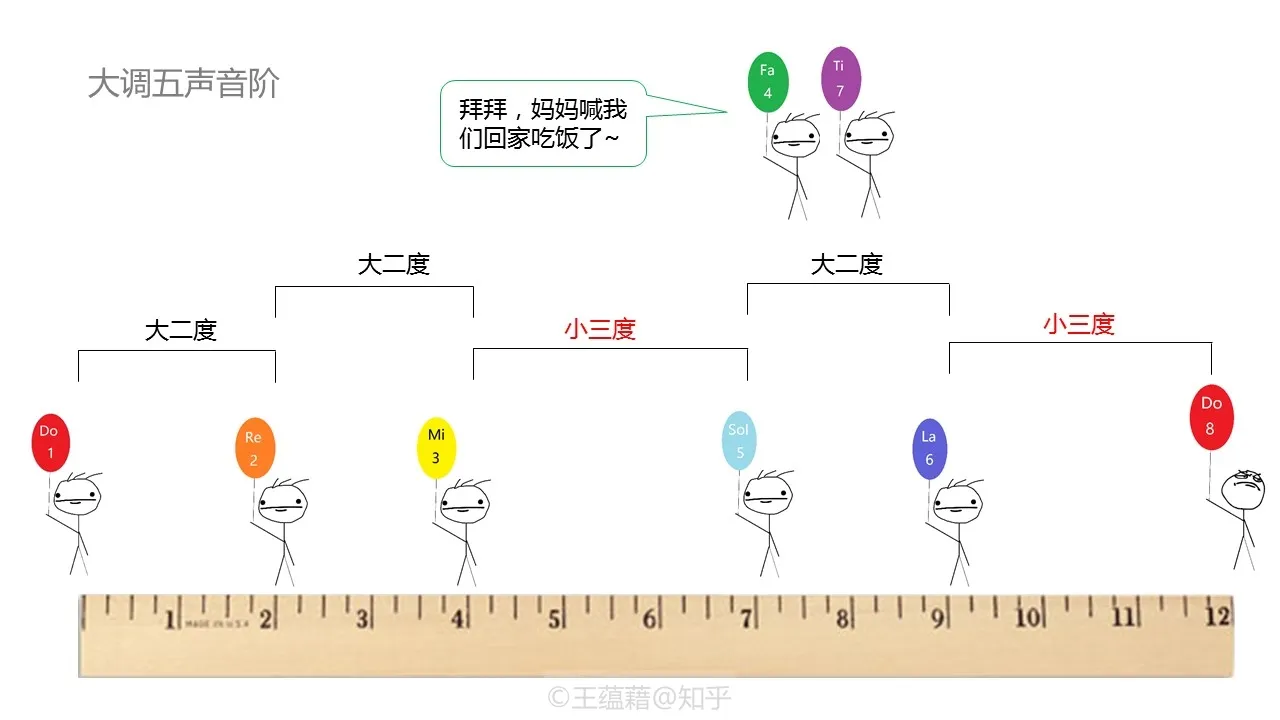
除了七声的自然音阶，历史上许多地区都独自开发出了五声音阶。

西方音乐中最常用的两款是由大调和小调衍生出的大调五声音阶和小调五声音阶，在乡村蓝调爵士摇滚等各种风格中都会用到。

• 大调五声音阶由大调去掉四级和七级音构成 1 2 3 5 6
• 小调五声音阶由小调去除二级和六级音构成 1 b3 4 5 b7。
• 五声音阶也存在关系调的概念，C 大调五声音阶（CDEGA）和 a 小调五声音阶（ACDEG）互为关系调。

在中国，我们对五声音阶有着更细致的区分，古代把 1 2 3 5 6 五个唱名分别叫做宫商角徵羽。五声音阶的五个音都能作为主音，因此可以产生宫商角徵羽五种调式音阶，不只局限于大调五声与小调五声音阶。

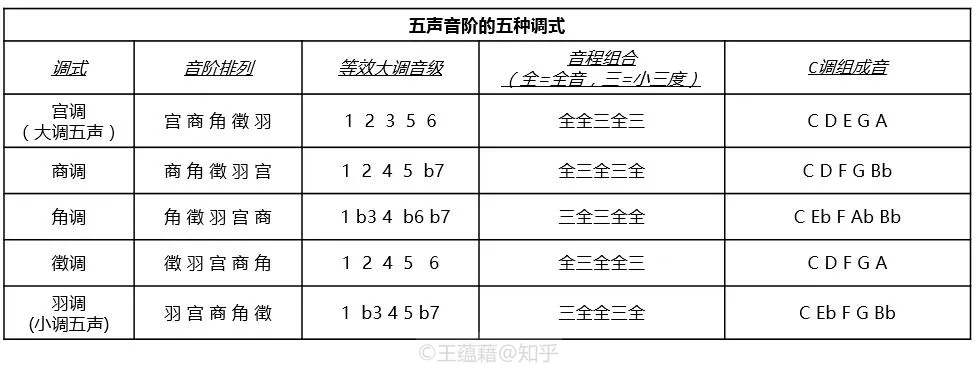
在即兴演奏中，五声音阶是最为保险的弹奏方式。仔细观察可以发现，大调五声音阶能在 Ionian，Mixolydian，和 Lydian 三种偏大调调式的音乐中使用，而小调五声音阶则可以套用在 Dorian，Phrygian，和 Aeolian 三个偏小调的调式上。因此大小调五声音阶的自由度相当高，即兴时很节省脑力，不用过多担心与和弦中的音打架。

大调小调五声音阶皆由大二度与小三度拼接构成，不存在半音程。任意双音组合中，除了大二度和小七度相对不稳定，其余则全是协和音程。而小二度，大七度，和三全音，这三种极不稳定的音程在大调小调五声音阶中根本不存在。因此，用五声音阶弹出来的曲子无论如何都不会难听，但是同时也不如自然音阶色彩丰富，处理不当容易显得单调乏味。

中国传统音乐曲目往往给人一种风轻云淡高山流水的感觉。其中一个重要原因就是曲子是基于上述五声音阶，在色彩上明显弱于大调小调，因此显得抽象疏离。和声功能的弱化，使得音乐表达情绪的任务更多承载在了音色，动态，以及其他演奏的细节变化上。因此，无论是古筝还是琵琶弹奏者，甚至是传统戏曲演员，想要将曲子演绎出味道，都需要深厚的基本功和丰富多样的演奏技巧或唱腔变化能力。

当然，中国音乐中也不仅仅只有五声音阶。《战国策》中有诗云：“高渐离击筑，荆轲和而歌，为变徵之声，士皆垂泪涕泣。”其中的“变徵之声”相当于在现代的大调五声音阶中加入了增四度音 #4，如此强的色彩音，怪不得能调动人的情感了。不过音律这东西，就和我国其他文化遗产一样，动不动就会失传的，还是五声音阶生命力顽强，一直流行于民间。

在流行歌中，如果和声上依旧沿用现代音乐手法，但旋律却以大调五声音阶的思维来构写，再配以一些民族乐器伴奏，就可以带来“中国风”的听感。不得不承认，节奏舒缓的歌谣配以协和的大调五声音阶对中国听众是极具吸引力的。周杰伦早期尝试过许多风格的曲子，比如《印第安的老斑鸠》这种迷幻爵士，《娘子》这种节奏蓝调与饶舌的结合，现在回顾惊为天人，但那时国内听众接受度却不是太高。而后来他在专辑中对中国风的尝试则极为成功，一曲《东风破》成功赢得了中老年人的关注和喜爱，使他一跃成为老中青通吃的全民偶像。由此可见一斑。

音乐是什么？

节奏、旋律及和声

音符与旋律

音乐最重要的三要素之一是旋律，旋律就是音乐当中的语句。

生动的文字会巧妙应用类比，引用，排比，对比等修辞的手法，而杰出美妙的旋律一样会用到这些技法。语言中，单词构成词组形成句子。音乐中的单词就叫做音符，而旋律就是由音符的组织出来的。旋律从音符、乐句、段落一直延伸还可以构建出乐章、乃至全曲。像这样在音乐中篇章的结构安排就叫做曲式。

让我们看一下简化了的五线谱，见下图。旋律中的音符随着时间的推移，先是维持在一个固定的音高，接着突然上升了一个较大的音程，接着缓缓下行直到又出现一个向上的跳渡，最后维持在一个固定的音高结束。

每一个音符都是由两个元素构成的：音高和时值。

• 音高决定了音符自身频率的高低也决定了音符之间互相的音高关系（即音程）
• 时值则是指音符的持续时间，时长越长的音符时值就越大。

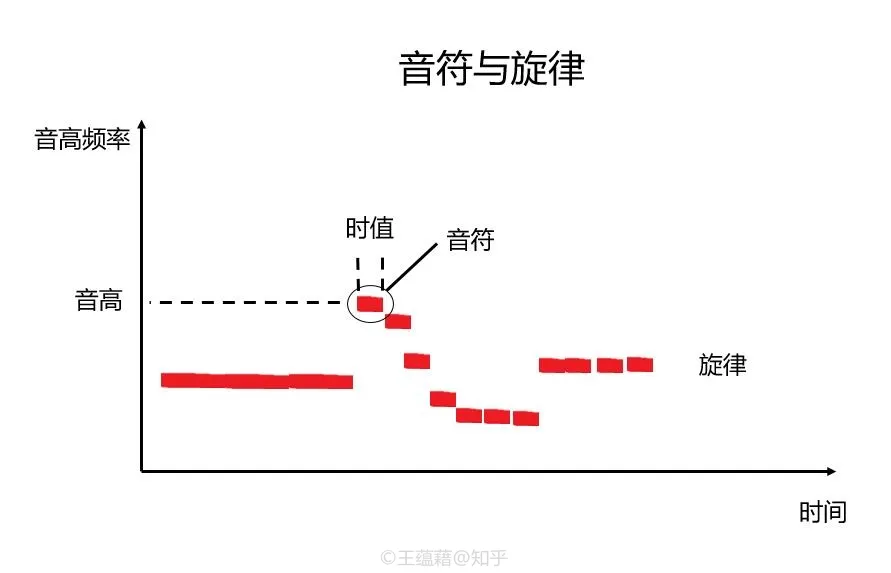
旋律是能给听众带来意义感的。大脑喜欢探究事物的意义和规则，而我们的听觉又非常灵敏，它能够辨识出音符走向。这使得我们具备了一个神奇的能力，能够像玩连线游戏一样，将分散的音符串联起来，听出有意义的旋律。所以，我们也习惯把旋律叫做“旋律线”。当然，不是所有的音符运动都能叫旋律的，就跟烂的作文不知所云不能被理解是一个道理。当然也不排除一些智商拔群创作者，故意不说人话，偏把音乐当做破译密码来玩弄。当我们无法分辨旋律时，音乐的含义就会模糊淡化，显得抽象。

如果你想作曲的话，除了在搜寻灵感之外，还值得关注以下几个方面。音乐家与学者们在研究一段旋律时，会关心旋律的走向（相邻音符之间的音程跳渡），旋律的音域范围，会关心整条旋律线的轮廓形状，等等。当然也不应为了理论而忘了旋律本身是否好听。

上一节我们介绍了音阶。其实，将旋律中用到的音符音高从低到高排列，就可以得到音阶。而反过来，从音阶中挑选一些音高在时间上横向发展就能组织出旋律。音阶就像一本新华字典，里面的沉淀了可以拿出来用的词汇；而旋律的创作和聆听就像是在写作和阅读文章，是赋予这些词汇生命的过程。

和弦与和声

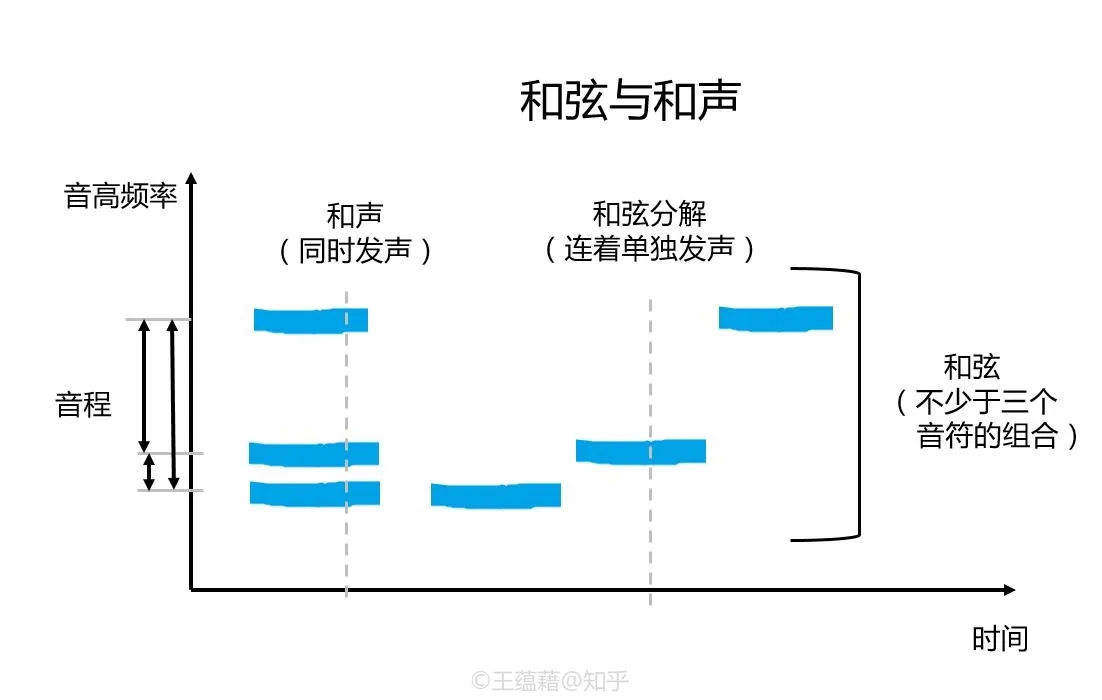
和声

音阶中的音横向发展得到旋律，而纵向发展就得到了和声。和声的推进变换会形成旋律，而多条旋律的叠加又反过来构成了和声。

音乐最重要的三要素之二就是和声。现代音乐概念里面，由多个不同的音高同时发声就形成和声。

如果说旋律是音乐中的语句，那么和声就是多个人同时在讲话，或者是某人在表演一嘴多舌的口技了。和声可以扮演音乐中的形容词副词，为旋律线增添五彩缤纷的色彩。

和弦

三个或三个音以上的和声就叫做和弦。一般来讲，和声的音符数量越多，其色彩就会越丰富。

和弦的音程关系远比双音复杂，多个音之间互相都会构成音程，音程组合的可能性随音高数量呈指数增长。

• 在过去的民谣和早期的古典乐中，和弦往往会用到最基础的由三个音组成的和弦，叫做三和弦。
• 而在现代流行音乐中，和声的色彩随着音乐的进化已经更为丰富，和声中往往会在三和弦的架构上再加入一到两个色彩音。
• 爵士乐则更进一步，这个风格的音乐中由五个六个组成音的和弦是家常便饭，即使是钢琴也需要两只手才能把和弦的音按全。

和弦中的音不仅可以同时弹奏形成和声，也可以先后连续奏出，这个过程叫做和弦的分解，或分解和弦。

在弹奏分解和弦时，我们依旧能隐约或强烈地感受到和声。由于大脑的短期记忆可以储存前几秒之前的音符并将这些音符拼接在一起，我们能够感受到分解音之间的音程关系，还原出和声的色彩。

同样，我们对旋律的感受也少不了大脑对相邻几个音之间的音程关系的处理。如果没有了短期记忆的帮助，我们恐怕就无法听懂音乐了。

节奏、节拍与小节

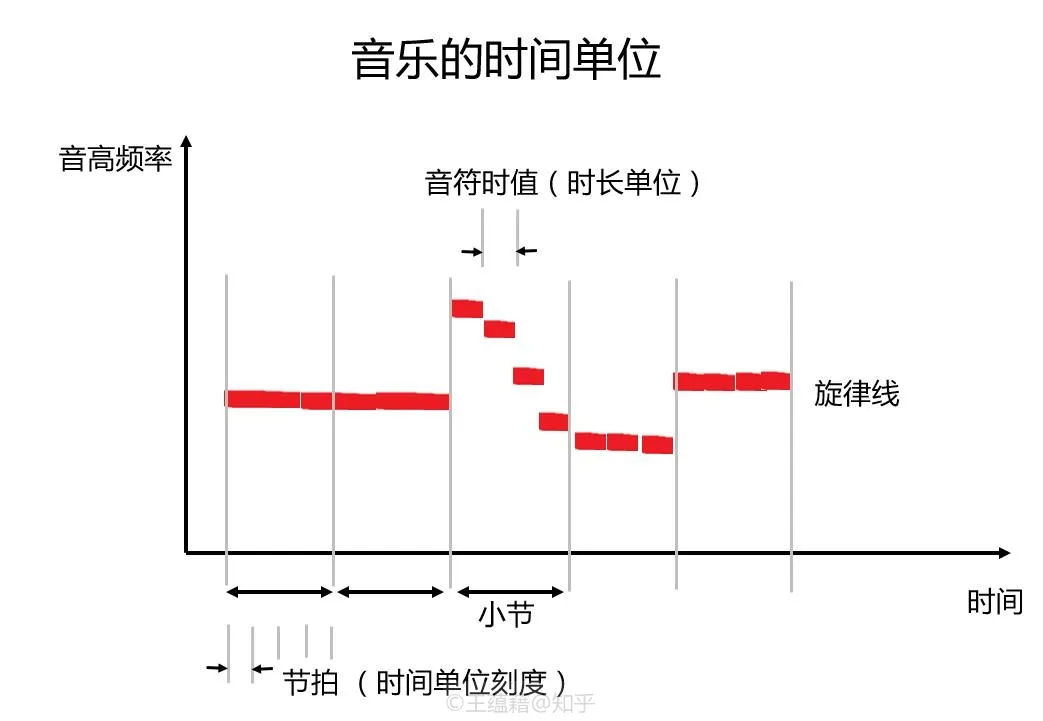
音乐最重要的三要素之三是节奏，即有规则有循环的律动。大脑痴迷于寻找规律和意义，节奏就是音乐在时间上的规律。规律性的节奏对大脑正中下怀，就连古人读书念经都是要摇头晃脑追求节奏感，其中便可见一斑。

将音乐量化分解成片段有助于我们看清节奏的规律，方便我们标记、分析、理解并记忆音乐。

• 就像音高可以用半音作为刻度划分，时间也可以用**节拍（拍子）**作为单位刻度来划分。
  • 音乐的速度快慢可以用每分钟节拍的数量来测算。
• 由于节奏中拍子的强弱变化呈周期性（嘭嚓嚓，嘭嚓嚓，嘭嚓嚓，~），我们可以把每一个周期的循环设定为一个小节。
  • 五线谱中像栅栏一样的竖线叫做小节线，它被用来分割一个个小节。
  • 每个小节里面拍子的数量被定义为拍型。一个小节有两拍的拍型就叫双拍子，有三拍的叫三拍子，以此类推。
  • 有时，对拍型的描述还包括小节中强弱拍的顺序关系。二拍子的拍型一般是“强弱，强弱，”，而四拍子的拍型常见“强弱中弱，强弱中弱，”。拍型的选择决定了我们如何感受韵律。

节拍与音符时值就像音名与唱名。节拍是音乐的时间刻度，它的时长是用音乐速度规定的。而音符的长短则是根据时值设定的，时值就像唱名一样是一个相对的概念，实际的时长可长可短。如同唱名需要和音名挂钩才能判断音高，音符时值也要和节拍绑定才能明确时长。音符时值的全长单位叫做全音符，一个全音符二等分得半音符，再二等分成得四分音符，继续切割可以得到八分音符，十六分音符，和三十二分音符。实践中，我们常常把四分音符或者八分音符的时值设定为一个节拍。

《小星星》五线谱上面的 4/4 代表拍号，拍号的分子对应小节的拍型：四拍子，而分母则是对应节拍和时值的关系：四分音符为一拍。可见，4/4 和 2/2 代表不同的含义，一个代表四个四分音符，另一个则代表两个二分音符，在乐谱标记时小节的划分是不一样的，对韵律的感受也不是不同的。它们的相同之处是每个小节中所有音符时值加在一起都正好等于一个全音符 4/4 = 2/2 = 1。当然，一个小节总的时值不一定是全音符，尤其是三拍子的节奏，比如 3/8 拍、3/4 拍。

乐谱上，我们常常还会看到像 6/8 拍、9/8 拍这样的复拍子拍型。复拍子就是拍子套拍子，具有多层结构。

• 比如 9/8 拍首先由三等份组成，每一份里面又是由三拍构成。
• 同样的，6/8 拍一般被看做一小节中有两等份，每一份又是由三拍构成的。

复拍子有助于我们更方便的感受复杂的节奏型。

与之相反，像 3/8 拍、4/4 拍这样分子由 2、3、4 构成的简单拍型被叫做单拍子。注意这里的“单”是和“复”相对应，“双拍子”和“三拍子”都被归类为“单拍子”。

以下是音符时值的五线谱标记，表中四分音符被设定为一拍：

由多个音符生成有规律的节奏组合叫做节奏型。节奏型与拍型不同，比如在一个 4/4 拍子的小节中，拍型就是四拍子，而节奏型却可以由十六个十六分音符构成。而且，节奏型中的音符的时值可以不一，可以发声也可以空着不发声。不发声的音符叫做休止符。

由四分音符 + 两个八分音符 + 两个四分音符可以构成一个节奏型，而下图中这个节奏型连续出现了两次。

舞蹈就是一门建立在音乐的节奏之上的一门艺术。许多与舞蹈同名的音乐风格在节奏上都有鲜明的特征，他们都有各自的速度、拍型和节奏型。

• 拉丁舞蹈和音乐的风格有伦巴，桑巴，恰恰等等，大多都是偶数拍子（如二拍子，四拍子）的舞蹈。
  • 恰恰舞在练习时有“踏~~踏~~恰恰恰！”的口诀帮助初学者踩对节奏，这便是节奏型的体现。
  • 伦巴是表现男女爱情的舞蹈，速度因此相对舒缓以承托柔美的舞蹈。
  • 而一提起桑巴，我们则会想起穿着如孔雀般鲜艳的巴西妹子热情洋溢的舞蹈，节奏那叫一个快。桑巴是二拍子的。
• 与偶数拍子的舞蹈不同，小步舞曲是三拍子的。古典音乐奏鸣曲式的一个乐章往往就会出现小步舞曲的曲式，而小步舞曲是在欧洲真实存在过的贵族舞蹈，只是后来不再流行。
  • 而现代仍旧流行的舞蹈中，华尔兹（圆舞曲）也是三拍子的。

音乐的织体

现在我们知道了音乐首要的三要素分别是：节奏、和声与旋律。三要素之间的结合方式叫做织体。就像织布有粗细薄厚之分，我们也可以感受到音乐织体的粗细与薄厚。虽然织体在乐曲中会不断变化，不过还是可以归纳出以下几种基本的模式：

• 像第一节中的图例一样，由一根旋律线单独进行地音乐织体叫做单调音乐。虽然叫做单调音乐，但是音乐本身并不一定单调。虽然织体的厚度最为单薄，但这种模式也有它的动人之处，比如妈妈为宝宝吟唱一首摇篮曲可以满怀深情。
• 由多个独立的旋律线并行构成的织体叫做复调音乐。复调音乐中，你可以同时听见不止一条旋律线。可见，即使是一个乐器也是可以演奏复调音乐的。
  • 但是，并不是多个乐器或多个声部演奏的音乐就一定是复调音乐。如果所有乐器声部都在演奏和模仿同一个旋律，这种织体被叫做支音音乐。
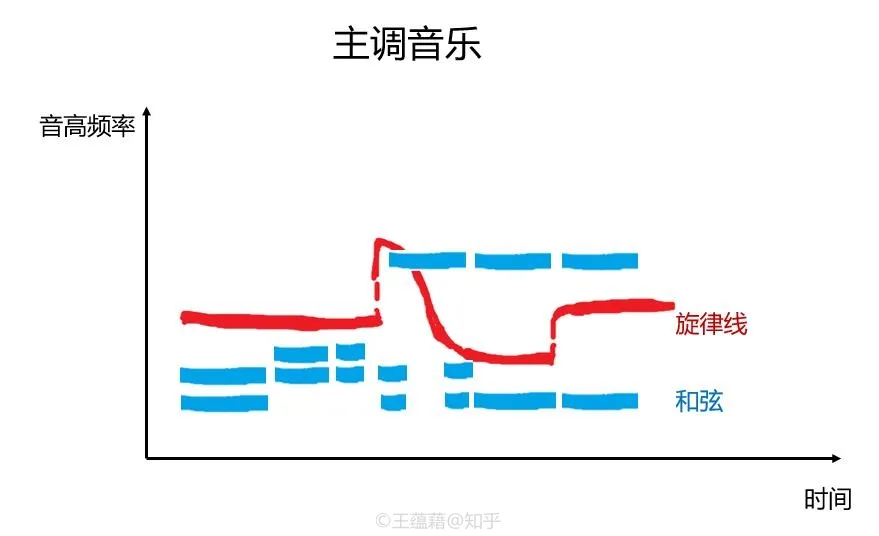
• 以上这些织体并不是流行乐中最常见的，我们最常见的织体叫做主调音乐。主调音乐织体是由一条旋律线配以和声进行来构成的。旋律中的音符即是和弦中的某个音，同时又可以构成一条独立的旋律。旋律音常常是和声中的高音，但这并不是绝对的，旋律也可以在低音或中音发展。
  • 与复调音乐不同的是，主调音乐和声中的非旋律音是用来衬托旋律并为其增色的，它们并不独立构成新的旋律线。而在复调音乐中，多条独立的旋律弦之间却可以互相构成和声关系，同时起到和声与旋律功能，这样的写作手法叫做对位法。由于对乐理知识要求较高，对位法一般是音乐专业学习者才会接触的功课，却也是严肃音乐中必不可少的技能和训练。

精心制作的流行乐中，往往会加入各种乐器和声效，为人声和主要乐器的空隙进行填充，就是为了避免产生织体厚度密度的骤变，除非本来就是要追求骤变的效果。交响乐团之所以需要庞大的编制，其中一个重要原因也是是对织体的考究，要求织体密度和厚度可以根据乐曲的需求来调整。比如多把提琴同时发声就要比一把琴声音更洪亮厚实。合唱团也是这个道理。

音高与音色

另一个交响乐团需要庞大编制的原因是对音色丰富性的追求。

每种乐器都有自己的声音特质，叫做音色。不同的乐器演奏同样音高的旋律时，我们之所以能将他们分辨出来，就是因为每种乐器都拥有不同的音色。

乐器演奏出的音符并非只有一个音高频率，而是有一组频率。

• 基频是这组音音高最低的频率，且往往最响。我们通常把基频定义为音符的音高。
• 而其他的高频则遵循一个规律，它们的频率都是基频的正整数倍，这些高频叫做泛音。

这个现象是由于物体振动模式导致的。正是这些掺杂进来的泛音使得乐器各自拥有了不同音色。如果没有泛音，所有乐器听上去都会像一个个音叉，音色无法区分。另外，这些音与音之间泛音的重叠也是和声之所以悦耳的关键，泛音重叠程度越高声音一般就越协和。

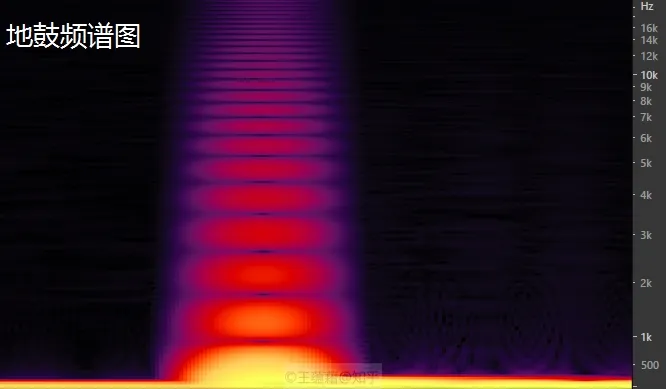
以上这种振动有规律，具有明显基频和泛音，能分辨出音高的声音叫做乐音，而振动没有规律无法清晰分辨基频泛音的声音则叫做噪音。

• 键盘管弦乐器演奏出来的一般都是乐音，而许多的打击乐如锣鼓就是噪音。
• 当然并不是所有打击乐器都是如此，比如木琴，定音鼓演奏的就都是乐音。

下图一是吉他单音演奏中的频谱图，图中可以清晰的看见基频和泛音。基频是最下面的音，在 0-500Hz 的范围，因为一弦的五品是 A440，我们大致可以猜测当时弹奏的是一弦或者二弦高把位的音。后面三个音的音高是稳定而有规律的。而第一个长音之所以升高又下降，是因为吉他推弦时，音高升高了大约一个半音的缘故。这些音明显都是乐音。而图二则明显是噪音，它是地鼓的模拟音，声音几乎覆盖了所有的频率，无法分辨基频在哪个频率。

强弱与衔接

每个人讲话风格和发音方式都不同。有的人讲话掷地有声抑扬顿挫，有的人说话平淡稳定，它们的区别在于发音力度的强弱选择不同。音乐演奏中对不同的强弱力度的使用叫做强弱法。

强弱的标记来自意大利文，*piano * 代表弱，缩写为 p，forte 代表强，缩写为 f。后来又细分出次强次弱等一些列强度。

好钢琴的原名就叫 piano forte，后来简写成了 piano。之所以这么叫是因为在钢琴发明之前，键盘乐器有一度按键的力度与演奏出来的音量是没有直接关系的，钢琴在强弱控制上能力，当时算是一种创新，故以此得名。

除了强弱，有的人吐字清晰具有播音范儿，有的人飙字如 rap，有的人咬字...（哎哟~不错哦），它们的区别在于字与字中间是如何过渡的。音乐演奏中，在音符连接上作的的处理叫做衔接。

• 比如断奏就是音符急促地发声之后立即静止造成音与音之间的衔接是断开的，这个特性使得断奏法可以体现紧张兴奋之类的情绪。
• 而连奏则正好相反，它让声音的过渡没有断裂，因此衔接变得柔顺悠扬，可以给人轻松舒畅的感觉。衔接的处理方式还有许多种。

如果说音乐三要素是音乐的内容，那么织体、音色、声音的强弱与衔接就是音乐内容的表达方式。表达方式不同，内容传达的效果也会不同。

和弦

听感：https://zhuanlan.zhihu.com/p/26146987

和声

欣赏音乐就像是在品味美食。餐桌上的每一道佳肴都由主食、配菜与调味料构成。音乐里面，旋律中的音符就是主食，而和声则相当于配菜与调味。就像没有加盐的鸡肉会嫌淡，没有配和声的旋律线听着也会觉得太清淡。恰当的和声可以增加音乐的“味道”，提升“口感”。

音乐当中的“味道”来自协和与不协和音程的配比。传统的和声一般是先从最协和的音程开始构建的。使用完全协和音程（纯四、五、八度）可以构建出双音组合，听觉上比单音更加厚实。这一招在中世纪的圣咏中就开始被用到了。

只用完全协和音程就像鸡肉外面裹了一层淀粉，虽然质地更厚，但是味道还是很淡。为了增添味道，音乐家发现和声上使用三度音程要比五度音程听着更为甜美，于是渐渐在作品中运用起来。

进入巴洛克时期，音乐家已经开始习惯同时在单音上添加三度和五度音来配置和声了。

• 三个音或三个音以上的和声就构成了和弦。
• 由一个单音开始，分别加入一个三度音和一个五度音就构成了基础的三和弦，而开始的单音叫做和弦根音。
• 完全协和的纯五度音起到了稳定和谐结构的作用，而不完全协和的三度音则提供了和声的色彩。
• 在巴洛克时期，最常用的和弦就是由大三度音和纯五度音构成的大三和弦，以及由小三和纯五度音构成的小三和弦。
• 大三和小三和弦的构成音之间都是协和音程。和弦的组成音无论如何颠倒排列都不会出现不协和的音程，因此十分悦耳。

下图是大三和弦的音程结构演示，所有音程都是由完全或不完全协和音程构成的。和弦的根音（root）用 R 标记，其他的和弦音级则用大调音级数字标记。

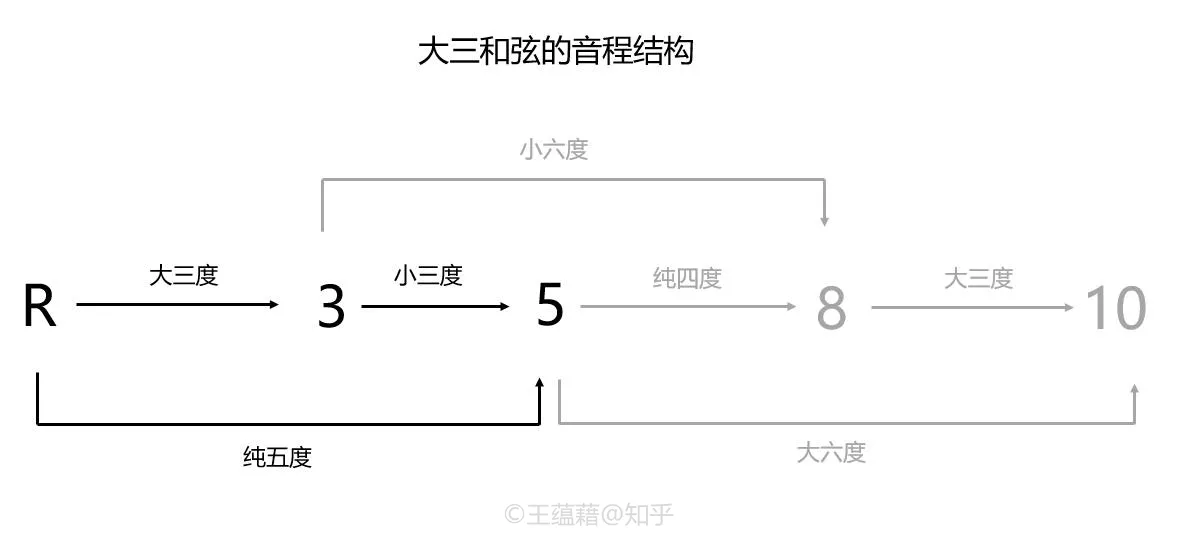
三和弦

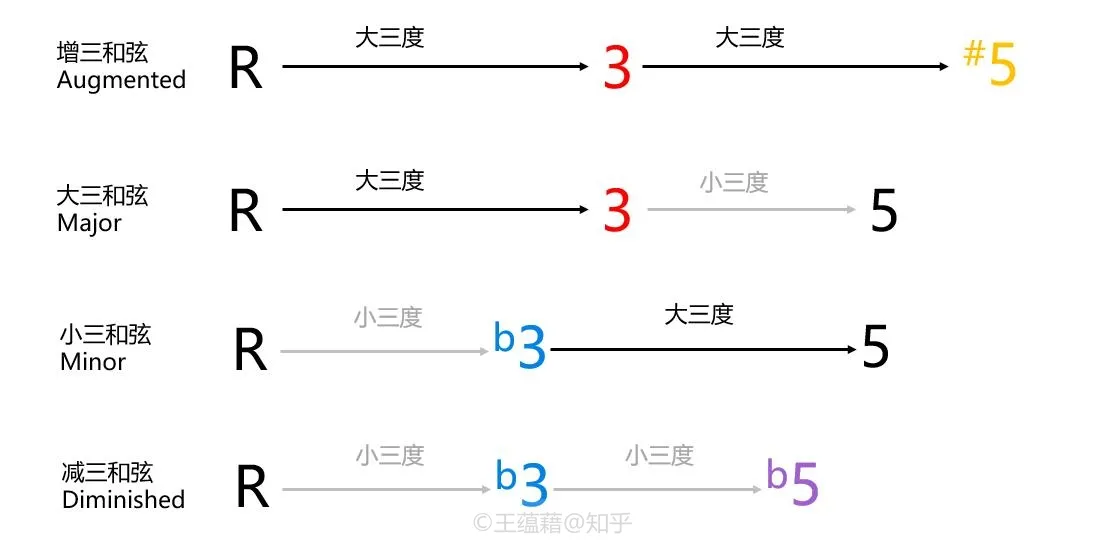
现代和声理论中，我们把三和弦定义为是由两个三度音程叠置出来的和弦，一共有四种属性：

• 用大三度叠加小三度就得到大三和弦
• 用小三度叠加大三度得到小三和弦
• 用两个大三度得到增三和弦
• 用两个小三度得到减三和弦

三音和五音的音程属性决定了和弦的属性以及听觉“色彩”或“味道”。

• 大三和弦与小三和弦的五度音都是协和的 5 音，听感愉悦舒适。
  • 将和弦单独拿来听辨时，大三度给人较为明亮开朗的感觉，而小三度则含蓄深沉。
• 而增三和弦与减三和弦的五度音则分别是不协和的#5 与 b5 音，声音有强烈的不稳定感。
  • 将和弦单独拿来听辨时，增三和弦具有悬疑紧张感，而减三和弦则有忧郁压抑的听感。

因此，增三与减三和弦使用的频率远远小于大三与小三和弦，甚至很多时候压根不会出现。

和弦可以按照属性进行标记以方便区分识别。和弦的标记一般是由根音的音名配上代表和弦属性的符号构成的。比如，有三个音 D F A，我们如果把 D 做为根音，那么 F 就是根音的小三度音，A 就是纯五度音。因此这三个音构成了一个以 D 为根音的小三和弦，记作 Dm 和弦。

和弦的标记法不是很统一，只有靠经常使用来熟悉记忆。

• 大三和弦一般可以直接用根音音名作为和弦名，也可以配以英文缩写 maj 或大写字母 M 字样表示；
• 小三和弦会在根音音名后加上减号 - 或英文缩写 min 或小写字母 m；
• 增三和弦一般跟加号 + 或英文缩写 aug；
• 减三和弦则跟圆圈 o 或者英文缩写 dim。

下图截取自 Wikipedia：和弦。

七和弦

当音乐家们听习惯并厌倦了三和弦之后，便开始尝试在和弦中添加更多的色彩音，挖掘更多音乐的可能性。浏览音乐史，我们可以发现随着时代推进，和声中不协和音程的使用变得越来越频繁。一开始听众对音乐家们的创新会感到不习惯，和声的改动会受到排斥或者忽视，但是渐渐当大众一旦开始熟悉并适应了新的和声效果之后，它就会流行起来。

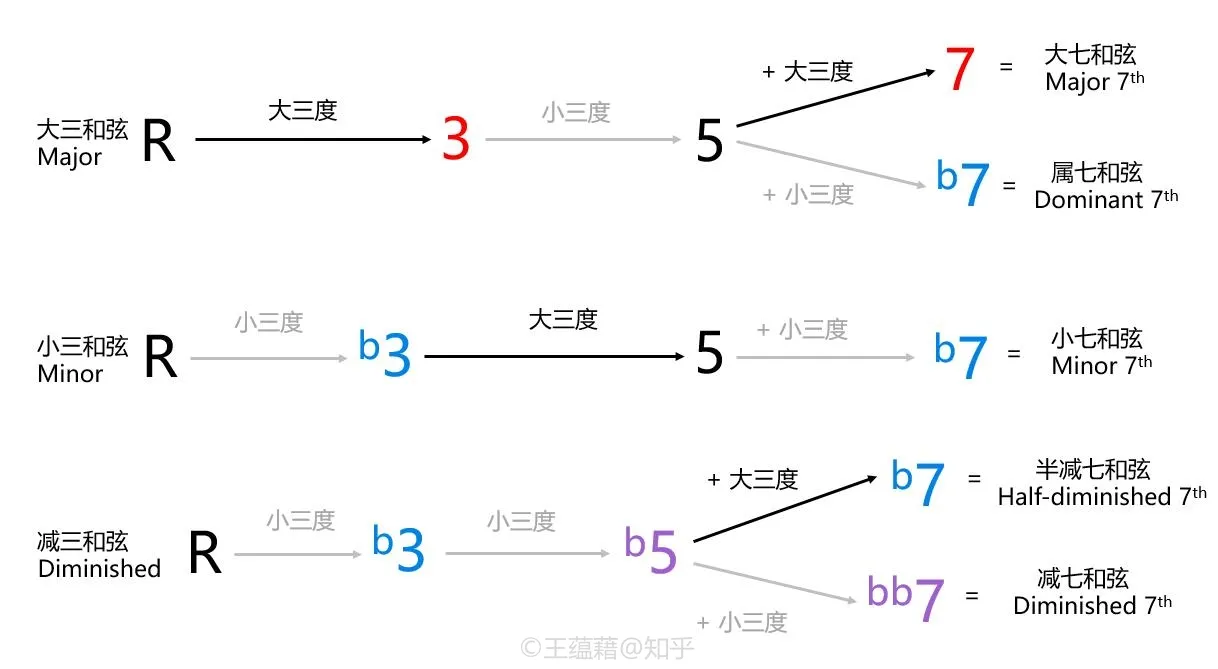
其中一个成功的尝试就是在三和弦的五度音上，继续叠置一个三度音得到七和弦。由于五度上方的三度音是七度音，故得名七和弦。虽然三和弦是由三个音构成，但是七和弦并不是。七和弦实际是由四个音组成，分别是根音，三度音，五度音，以及七度音。

我们可以通过两种角度来理解和记忆七和弦的音级和音程关系。首先七和弦是由三个三度音叠置构成的。其次，当我们熟悉了三和弦的结构之后，七和弦可以看做是用三和弦叠加一个七音构成的。另外，七和弦之间也可以相互之间进行比较来加深印象。

以下是五种最常用的七和弦，初学者不必贪多，可以从前三种开始记忆：

• 大七和弦 R 3 5 7，常记作 maj7，如 Cmaj7。
  • 大三和弦 + 大七度音
• 小七和弦 R b3 5 b7，常记作 min7 或 m7，如 Dmin7 或 Dm7。
  • 小三和弦 + 小七度音
• 属七和弦 R 3 5 b7，常记作 7，如 G7。
  • 大三和弦 + 小七度
  • 介于大七和弦和小七和弦之间
  • 属七和弦与小七和弦的区别在于三度音，与大七和弦的区别在于七度音。
• 半减七和弦 R b3 b5 b7，也叫小七减五和弦，常记作 m7b5 或 ø7，如 Bm7b5 或 Bø7。
  • 减三和弦 + 小七度音
  • 在小七和弦的基础上还降低了五音。
• 减七和弦 R b3 b5 bb7，常记作 dim7 或 o7，如 Bdim7 或 Bo7。
  • 减三和弦 + 减七度音
  • 比半减七多降了一次七音。
  • 有意思的是 bb7 与 6 是异名同音，谱子上虽然标记七度音程，但是实际乐器演奏时用到的却是和大六度一样的音。

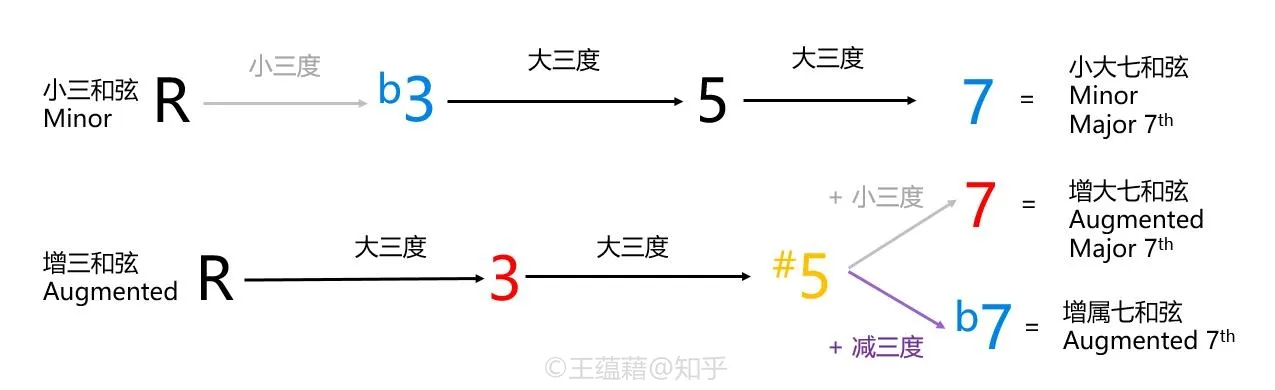
此外，还有三种较少用到的七和弦也列在下面供参考。它们可以分别从大、小、属七和弦中变化某一个音来获得，听感上都不太协和。

• 小大七和弦 R b3 5 7，常记作 mM7，如 CmM7。
• 增大七和弦 R 3 #5 7，常记作 maj7#5，如 Fmaj7#5。（也可标记为 +M7，如 F+M7）
• 增属七和弦 R 3 #5 b7，常记作 7#5，如 G7#5。（也可标记为 +7，如 G+7）

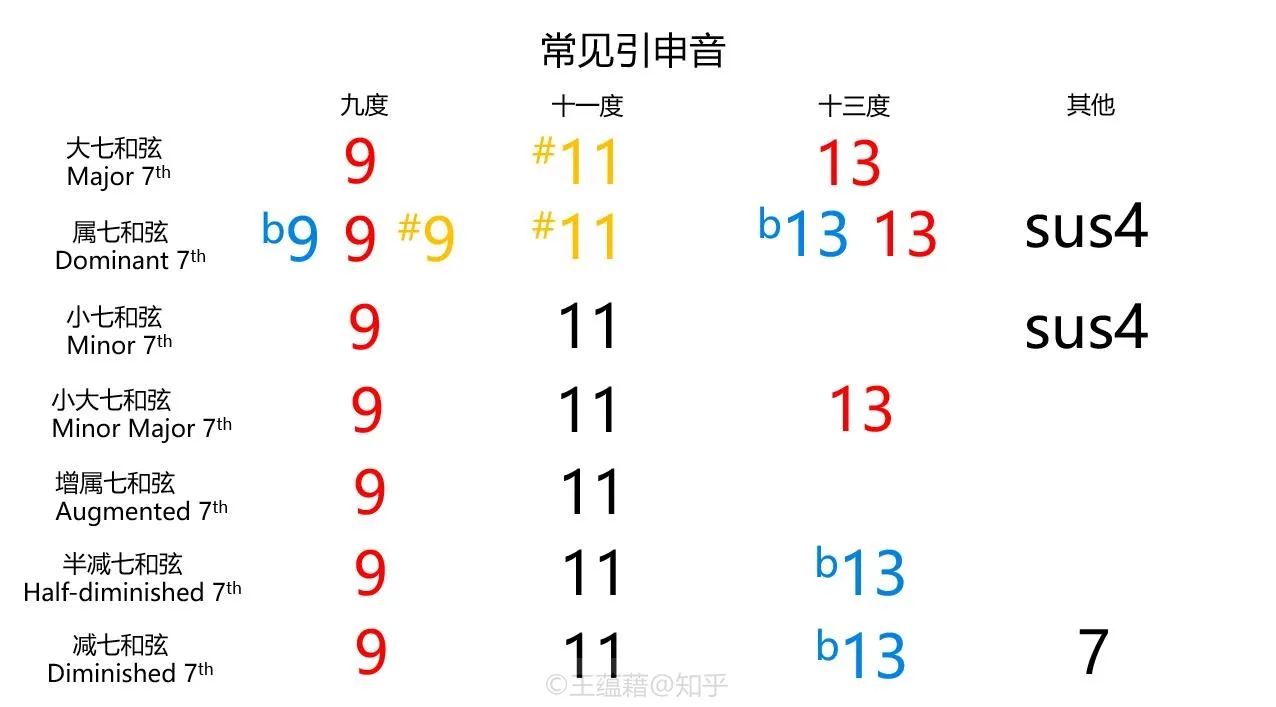
引申音与和弦外音

当然，音乐家对三度音程堆叠的尝试并未止步于七和弦。由七和弦继续往上叠置还可以得到九和弦、十一和弦、十三和弦三种引申和弦，标记时将七和弦原有数字 7 改写成 9,11,13。

十三和弦由七个音组成，它可以囊括七声音阶中的七个组成音。比如 Fmaj13(#11) 和弦就是由 R 3 5 7 9 #11 13 度音 F A C E G B D 构成的，它们恰好是 C 大调的七个构成音。可见这样高叠的复杂和弦自己已经俨然演变成一条音阶了。（当然十三和弦并不是和声堆叠的终点，平均律里可是有十二个音呢！但是我们就不必研究了。）

由于引申和弦在爵士乐中司空见惯，而现代流行乐的和声中越来越多地融合了爵士的风格，我们不可避免地会在歌曲中遇到这些引申和弦。有时，为了制造惊喜的效果，歌曲也会偶尔用到这些特别的和弦。因此，我们有必要对引申和弦的概念有所了解。

为了方便理解和归类，对于超过七和弦范围的复杂和弦，我们可以把它们看做是由七和弦的四个组成音作为框架并搭配和弦外音构成的和弦。九、十一、十三度音都被看做是七和弦的和弦引申音（延伸音），并不作为和弦本身的框架。

• 比如 Fmaj13(#11) 和弦就是由 Fmaj7 和弦搭配 9、#11、13 三个音的十三和弦。和弦标记中，括号中的内容是为了指明了十一度音是 #11 而不是还原 11。
• 像 #11 这样带有变音记号的引申音叫做变化引申音。如果引申音没有升降记号，则可以省略括号，如 G13。和弦标记中，数字反应了最顶层的引申音的音级。

所有非和弦框架内的音都叫做和弦外音，其中包括引申音。由于实际应用中，经常不太在意和弦外音是在高八度还是低八度，所以我们可以把和弦外音二、四、六度音都看做引申音九、十一、十三使用。

省略弦内音

由于太多音同时发声会使得和弦属性变得模糊浑浊，所以实际中并不是所有和弦内音都会被弹奏出来。

• 首先，在七和弦框架内部，大七、小七、属七的纯五度音 5 由于过于协和且并不提供区别和声属性的功能，所以可以被忽略，只留下和弦的根音、三音、七音。
• 而在半减七和弦中 b3 则可以被忽略，R b5 b7 足以使它和小七或减七和弦进行区分。
• 其次，如果没有特别强调，在七音与最顶层的引申音之间的其他引申音是可以省略的。
  • 比如在 Fmaj13(#11) 中，除了五音可以省略之外，介于 7 和 13 之间的 9 音是可以被忽略的。但是由于#11 音被标记出来，此处不能省略。简化后的和弦就只有五个音了，分别是 R 3 7 #11 13。

使用 add 明确引申音

如果需要明确和弦的引申音，则可以启用 add 字样或者括号在原有和弦结构上具体标明引申音

• 比如 Cm7add11add13（no5），Cm9add13 就分别是省略了 9 音和 11 音的 Cm13 和弦，它们也可以用括号表示为 Cm7(11,13,no5) 以及 Cm9(13)。括号中的 no5 明确表示要省略五度音。

当和弦本身不具备七音，我们可以把它看做是由三和弦作为框架并搭配和弦外音（或引申音）得到的和弦，用 add 字样标识，如 add2，add4，add6 或 add9，add11，add13。

• Amadd9 就是加了 9（2）音的 Am 和弦
• Cmadd11 就是加了 11（4）音的 Cm 和弦
• 注意，add9 与 9 和弦的区别就在于 add9 中没有 7 音。

在流行乐和爵士乐中，大三和弦基础上的 add6（或 add13）和弦常常简写为 6 和弦，小三和弦的 add6 简写为 m6 和弦，而 add6add9 和弦则分别简写为 69 和 m69 和弦。比如：Eb6 或 Ebm69。（注意这里 Eb6 的含义是 Eb 的加六和弦，而不是 E 的加降六和弦。加降六和弦不能省略 add 记号，应该写成 Eaddb6 或 Eaddb13。）

避免音

虽然在命名时可以使用任何音名组合，但是在实际构建引申和弦时，我们需要考虑和弦好不好听，因此不是每个音都可以与七和弦搭配的。尤其是当它们是在七和弦的组成音上方的小二（九）度时，听感很不协和，这些音叫做避免音，一般不会放进和弦中。另外，当一个音会严重混淆和弦的属性时也需要避免。

• 9 比根音高全音，因此在任何七和弦中都适用。而 b9 和 #9 则只能搭配属和弦这一个特例。
  • #9 要避免的原因是它和 b3 异名同音，它会扰乱大七和弦三度的属性，而小七和弦本身就含有 b3 了。
  • b9 则与根音是小二度关系，听感不和谐
• 11 可以适用于任何基于 b3 的七和弦，但是 11(4) 与 3 冲突，因此在大七与属七和弦中应该使用 #11 代替。
  • 属七和弦若要用 11 音，则需要舍弃 3 将和弦变成属七挂四和弦。
  • 除了 11，其他所有的引申音都适用于属七和弦。
  • #11 适用于大七与属七和弦，它和半减七和弦中的 b5 异名同音，不适用小七和弦。
• b13（b6）与 5 冲突，除了属七和弦中可以省略 5 并把 b13 当做#5 看待之外，就只能用在减七或半减七和弦上。
  • 13 比 5 高全音，因此在大七、属七和弦都能适用。
  • 对于在小七和弦上用 13，不同人对此态度不一。有的人觉得 m13 听感太不协和，和弦属性过于模糊，13 应该当做避免音，具体要根据个人喜好决定。

避免音的设定是约定俗成的习惯，为的是避免不当心弹出过于突兀的和弦。如果音乐本身就需要不协和或是和声属性模糊的和弦，则可以摈弃避免音的限定。

除去了避免音之后，以下是和弦常见的引申音。

非三度叠置的和弦

和声学发展到现在，和弦概念早就被解构和重构很多次了。基于三度堆叠的和弦思维，仅仅是理解和声的茫茫可能性中的一种，只是它恰好被最多的人接受罢了。“其实地上本没有路，走的人多了，也便成了路。”

除了向更高的三度堆叠，音乐家也尝试突破和弦本身三度堆叠的教条，使用非三度的方式构建和弦。

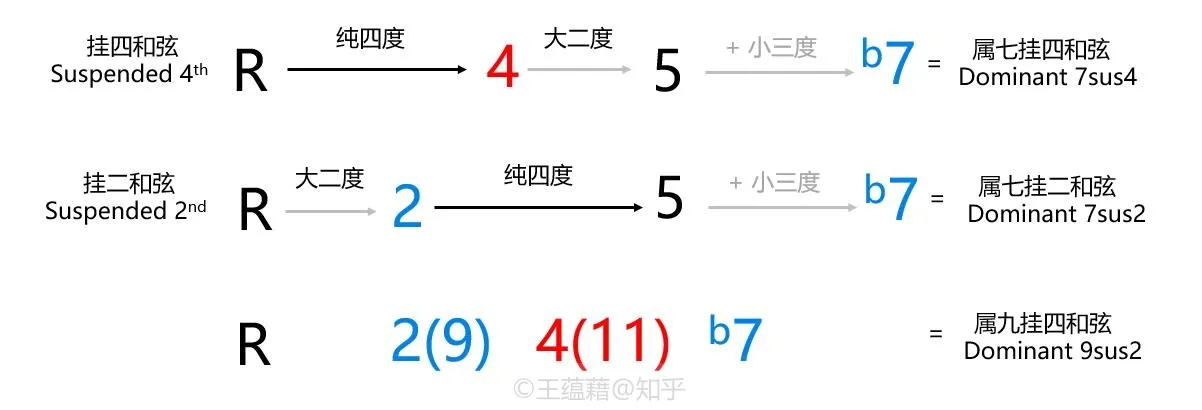
挂留和弦

其中一个例子就是挂留和弦。挂留和弦保留了大三和小三和弦中的根音和纯五度音，却把三音修改为大二度音或纯四度音，音程也由大三度和小三度的叠置变成了大二度与纯四度的叠置。

挂二和弦用 sus2 表示，挂四和弦用 sus4 或 sus 表示，如 Gsus4。

挂留和弦的挂留音就像被悬在空中等待着陆一样，具有回到三度音的倾向。这是因为音程中大二度的稳定性弱于大三和小三度。大二度在古典乐中一开始甚至被认为是不协和音程，挂留音出现后必须要回到三度音。发展到后来大二度才被认为是协和的。

由于没有了三度音来区分和弦的色彩属性，挂留和弦的听感上比较空灵抽象，很多现代流行乐中往往将挂留和弦独立使用，挂留音不再必须回到三度音。

挂留和弦也可以普及到七和弦中形成属七挂四，属七挂二，以及同时拥有挂二和挂四音的属九挂四和弦。分别用 7sus4、7sus2、9sus4 表示。

四度叠置

另外，有一批音乐家引领了四度叠置的和声的开发实践，以四度代替三度堆叠的和弦构建方式。

这里说的四度音程，一般是指纯四度或增四度。四度叠置的和声听觉色彩与三度完全不同，由两个纯四度堆叠出 R 4 b7 的组合正好是一个属七挂四和弦，听觉上同属七挂留和弦一样很抽象。虽然再往上叠置四度可以得到 b12 音（高八度的 b3），但是此时的小三度音由于是在高八度，已经像是属七挂留和弦的引申音了，与它在三和弦中塑造的听感效果已经很不一样了。

强力和弦

摇滚乐中的强力和弦也不符合严格意义上的和弦定义，它实际只包含根音和纯五度音。标记时一般在根音后跟上数字 5，如 D5。原因大致有二：

• 首先，由于电吉他加入了失真效果会产生出原信号中本不存在的高频频率，而十二平均律调弦得到的三度音音高倍数与 5/4 倍差异较大，在大量失真效果处理后会带来很多不纯的音程，声音听上去显得杂乱模糊并干扰到旋律，因此三度音被舍弃在了强力和弦之外。
• 其次，五度则基本接近根音的 3/2 倍，频率上与根音可以很好地融合，而且完全协和音程的叠置也使得声音听上去厚实坚硬，正好符合摇滚乐手想要追逐的具有冲击感的效果。

强力和弦相当于只提供了根音位置，而没有提供和声的色彩属性。和声的色彩属性需要经由和弦根音与旋律线或者其他声部中的音符共同决定，聆听时要将音乐整体结合起来才能听辨和弦的属性。

大调的使用指南

⭐ 大调音程结构

首先，让我们回顾一下大调的音程构造。

二度与七度

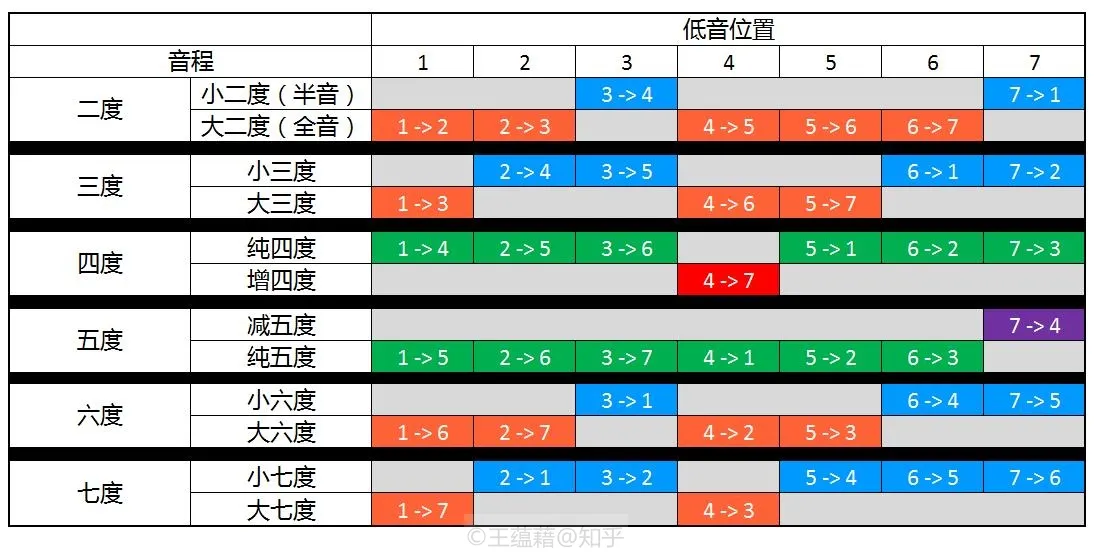
从二度关系来看，大调是从主音 1 向上由八度中七个不同的音以 全全半全全全半 的音程组合构建而成的。

• 大调中有两对半音程关系（也就是两组小二度），分别介于 3 和 4 以及 7 和 1 之间。
• 而这两对半音程的边上，分别有一组由连续两个全音构成的音阶 123，以及一组由连续三个全音构成的音阶 4567。

而七度关系是颠倒了的二度关系。大调中含有两组大七度，分别是 1 和 7 之间，以及 4 与 3 之间，是二度中两组半音关系的 “镜像”。而其余的五组七度音程皆为小七度。

三度与六度

三度关系的重要程度仅次于二度关系。

• 大调中有三组大三度，分别是 1 到 3，4 到 6，以及 5 到 7。尤其注意，这三组大三度的低音位置分别是 1、4、5 这三个数字，它们接下来会有重要任务。
• 大调的其余四组三度音程都是小三度。

而六度关系则正好是三度关系的“镜像”。

四度与五度

大调的四度关系与五度关系很好记，两者亦互为“镜像”。

• 4 与 7 互相之间构成了三全音关系，从 4 到 7 音程向上为增四度，而 7 到 4 音程向上为减五度。注意增四度与减五度都等价于六个半音，或者三个全音（故名“三全音”）。
• 大调中的其他四度与五度关系则皆为纯音程。

经过上面一番梳理，大家觉得大调的音程结构有没有好记一些了呢？对于初学者，一开始只需要记住以上提到的两组半音，三组大三度，以及一对三全音，便可以通过简单逻辑推倒出大调中任何音和音之间的音程关系了。当然，我们最终希望能将大调的音程全部内化为潜意识。

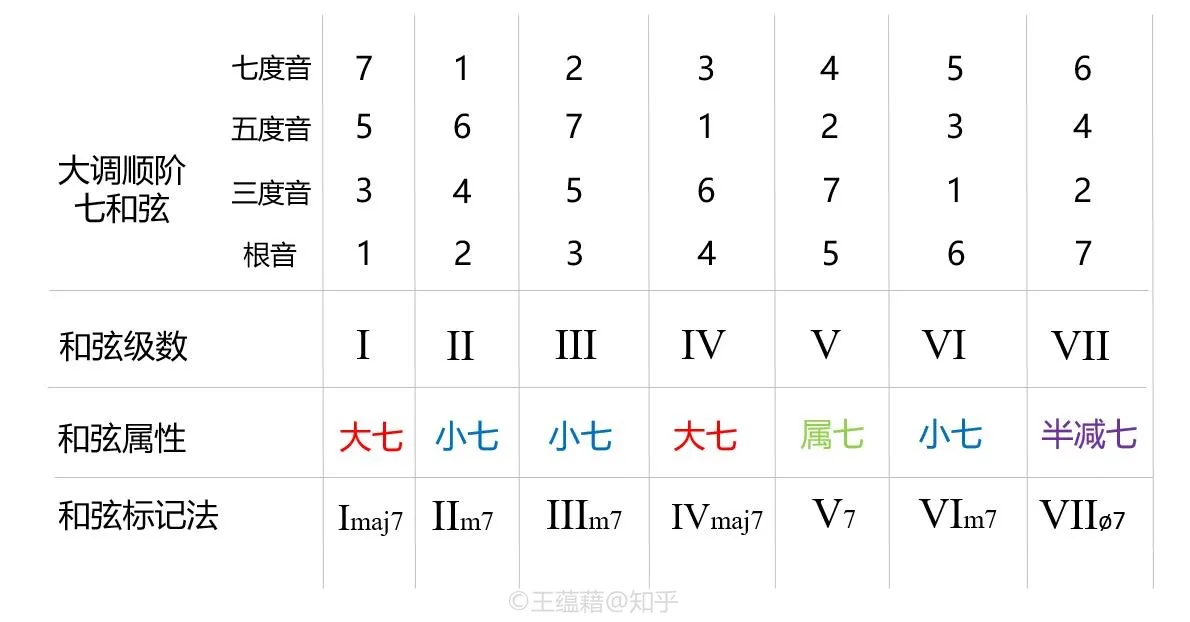
调内顺阶和弦与和弦级数

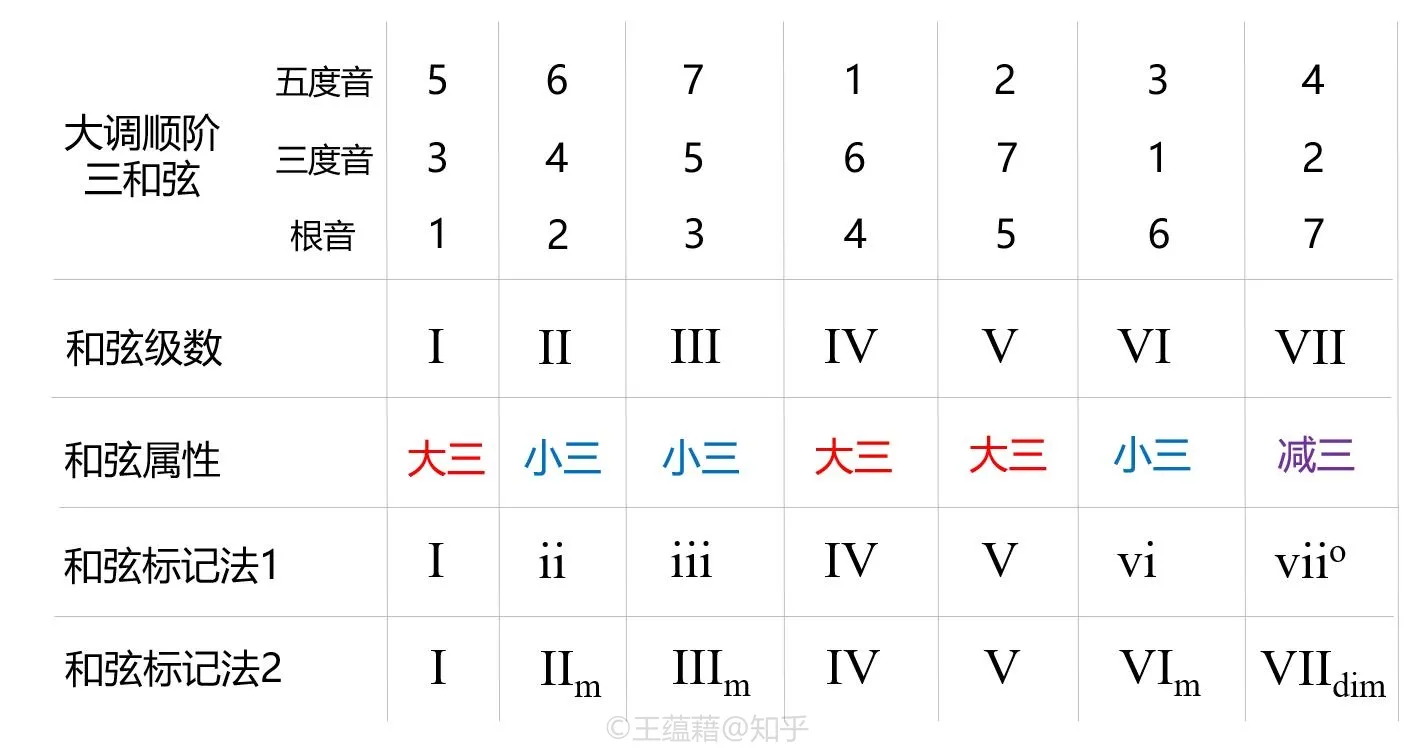
接着，我们来观察一下大调里面所包含的和弦。在第八讲中我们知道了，和弦是从根音向上用三度音程叠置得到的。大调的每一个音级上都可以构建出一个由大调音阶中的音来组成的和弦，这些和弦叫做大调的调内和弦或顺阶和弦。

顺接三和弦

和弦中最基础的一类是三和弦，大调中的顺阶三和弦一共分三类。第一类是由大三度叠加小三度构成的大三和弦。上一节我们观察到，大调中存在三对大三度关系，低音分别在 1、4、5。由这三个音为根音组成的和弦恰好就是大三和弦。

和弦与大调主音之间的位置关系可以用和弦级数标明，一般用罗马数字标记，和弦的级数由根音所在的音级决定。

1，4，5 三个大三和弦和弦级数分别是 I、IV、V。I 级和弦由 1 3 5 构成，IV 和弦由 4 6 1 构成，V 级和弦由 5 7 2 构成。

在大调与小调中， I、IV、V 级和弦地位非常重要，因为这三个级数上的和弦结合起来就能够定义完整的音阶了。传统乐理中会把这三个和弦统称为正三和弦。

第二类顺阶三和弦是小三度叠加大三度构成的小三和弦。大调中有三组小三和弦，和弦级数分别为 II、III、VI。II 级和弦由 2 4 6 构成，III 和弦由 3 5 7 构成，VI 级和弦由 6 1 3 构成

大调中最后一类顺阶和弦是由小三度与小三度叠加构成的减三和弦。VII 级和弦是大调中唯一的减三和弦，由 7 2 4 构成。

✔️ 结合起来看，大调 1-7 级上的顺阶三和弦的属性依次为大三、小三、小三、大三、大三、小三、减三。这个顺序是大调的普遍规律，无论是 C 大调还是 G 大调，顺阶和弦的属性都符合这个规律。

级数和弦的标记法

使用级数来标记和弦属性时，可以遵循第八讲中介绍的和弦标记法。级数和弦（或数字和弦）常见有两套标记法：

• 第一种标记法中，大三和弦用大写罗马数字表示，如 IV。增三和弦在大写数字后配以＋号，如 I+。小三和弦使用小写数字，如 ii。减三和弦则在小写数字后配以 o 号，如 viio。
• 第二种标记法中，和弦全都使用大写罗马数字标记。大写数字后，大三和弦不配任何符号，增三和弦配以 aug 或 + 号，小三和弦配以 m 或 min，减三和弦配以 dim 或 o 号。

两种标记法各有各的优劣，选择上以表达清晰为准。七和弦与引申和弦等其他和弦的标记法请参考第八讲。

顺接七和弦

知道了顺阶三和弦，下面我们来了解一下大调顺阶七和弦。顺阶七和弦一共有四类，比顺阶三和弦多出一类。其中，三个小三和弦加入七度音后都变成了小七和弦，减三和弦则转化为了半减七和弦（注意，不是减七和弦），I 级和 IV 级的大三和弦变成了大七和弦。

奇妙的是，V 级和弦并非大七和弦，而是属七和弦，它的七度音 4 与根音 5 之间是小七度。由于大调顺阶和弦中只存在一种属七和弦，知道了属七和弦的构成音，就可以明确大调音阶中的其他音，因此属七和弦在确定调性时起到了关键性的作用。

结合起来看，大调 1-7 级上的顺阶七和弦的属性依次为大七、小七、小七、大七、属七、小七，以及半减七。

和弦级数的应用

一旦掌握了和弦级数的概念，我们就可以把它套用到不同的调上面，迅速找出各调顺阶和弦的名称了。

以 C 大调为例，C 大调的 1-7 级分别是 C D E F G A B，其对应的和弦名称如下图。如果你有钢琴或吉他和弦演奏经验，那么你一定已经对 C 大调前六级上的三和弦不陌生了，它们分别是 C、Dm、Em、F、G、Am。而 Bdim 由于不协和感太强，许多歌曲中会避免使用，反而加入七音后的 Bø7 弱化了不协和感，使用频率更高。

不仅 C 大调可以用和弦级数推算出和弦名称，其他的大调中的和弦也可以用同样方法很方便地算出来。无论是哪个调，大调每个音级上的和弦属性都是确定的。

下图展示了 G 大调的顺阶和弦。我们可以观察到，G 大调的顺阶和弦与 C 大调的顺阶和弦是有重叠的。两个调中都使用到了 C、Cmaj7、G、Am、Am7、Em、Em7 这几个和弦，只是它们在两个调中的级数完全不同。而类似 Dm7 与 D7 这样同根音却不同属性的和弦则把 C 调与 G 调区分开来。

在知道歌曲调性时，我们也可以反过来根据和弦名称推算出对应的和弦级数。比如在 G 大调中，Am 和 D7 分别是调内的 ii 和 V7。

一旦掌握了正反两种推算能力，我们便可以通过使用和弦级数来轻松完成歌曲的变调了。**变调（移调）**就是将一首音乐从一个调整体平移到另一个调。变调前后，和弦与主音的相对位置关系是一样的，因此和弦的级数不会发生改变。

假设有一首 C 大调的男声歌曲，现在想改成 G 大调来适应女声的音域。原曲中用到了四个和弦 C、Am、F 和 G。想要将这四个和弦由 C 大调改成 G 大调，我们可以首先算出这四个和弦在 C 大调的级数是 I、vi、IV、V，然后再在 G 大调中找出级数所对应的和弦，它们分别是 G、Em、C 和 D。变调后弹奏这四个和弦即可。

✔️ 调的判断

上一节提到，不同的调可以享有同一个和弦，这会引申出一个问题：如何通过和弦来确定歌曲的调性？由于大调与小调歌曲风格色彩差异明显，不容易混淆，因此本讲将只着眼于大调，默认曲子是由大调谱写的。我们会在下一讲来介绍如何确定小调歌曲的调。

要确认大调歌曲所在的调，我们必须知道不同属性的和弦分别在大调的哪几个级数上面。

• 首先，由于大调中只存在一个属七和弦以及一个半减七和弦（或减三和弦），因此当属七和弦或半减七和弦出现时，调的选择只可能有一种。比如看到 D7 时，我们知道它只存在于大调的 V 级，所以这首大调歌曲是 G 大调的。而 C#ø7 只可能是大调的 VII 级，它所对应的调为 D 大调。
• 其次，大调中只存在一对间隔全音的小三或小七和弦。比如当看见 Fm 与 Gm 时，我们可以迅速判断出这两个和弦分别是大调的 II 级和 III 级，因此曲子的调为 Eb 大调。
• 同样，大调中也只存在一对间隔全音的大三和弦。因此当看见 D 和 E 和弦时，我们可以判断它们是大调的 IV 级和 V 级，所以曲子是 A 大调的。
• 另外，大调中只存在一对由大三和弦与其上方五度的小三和弦构成的组合。当 A 与 Em 同时出现时，可以肯定这两个和弦分别是 D 大调的 V 和 ii。

其他的情况下，大调的调可能无法由一到两个和弦确认，但我们至少能够将这些可能性迅速缩小。比如，一个大七和弦只可能隶属于两种大调，在其中扮演 I 级和弦或 IV 级和弦的角色。比如拥有 Fmaj7 的大调只可能是 C 大调或 F 大调。以此类推，小七和弦也只可能是三种大调中的 II、III、VI 级。

不止和弦属性可以用来判断调性，旋律中的音程关系也有同样功效。半音程以及三全音都可以将大调的选择性缩减为两种。比如，G#和 A 既可能是 E 大调的 3 和 4，又可能是 A 大调的 7 和 1。又比如，F 和 B 既可能是 C 大调的 4 和 7，又可能是 Gb 大调的 7 和 4（此时 B 实际上写作异名同音的 Cb）。

当然，以上方法只适用于歌曲没有转调或使用到调外音或和弦进行离调的情况。转调是指在歌曲内部调性发生了长期的改变，而离调是指歌曲的和弦或旋律短暂地离开了原有的调。如果曲子转调了或用到了非顺阶和弦使歌曲离调，那么我们就不能直接简单套用上述的判断方法了。我们需要先找出歌曲转调或离调发生的位置，将歌曲根据这个位置进行切割，然后分别来分析原调与新调的调性。

调性音乐

第六课在介绍西方音乐体系时说到了调性音乐，调性音乐是以大调小调这两种调为模板框架来写作的音乐体系，共有 24 种调，大调小调各 12 种。“大调”这个名称就来自调性音乐。也正是从调性音乐开始，音乐在和声上开始使用以三度叠置构建而成的和弦。在调性音乐里，每个音级上的顺阶和弦都扮演着特定的角色功能，不同功能的和弦按照一定规则衔接时，会从听感上形成一个明确的主音位置，或者说确立一个稳定的调性，故得名“调性音乐”。

调性音乐的和声是围绕着主音上的和弦推进的。在音乐中，随着时间推进变化出的一系列和弦被称为和弦进行。

• 主和弦（一般指三和弦）由 1 3 5 三个音级构成。
• 从主和弦出发，和声在推进演变过程中会逐渐偏离主和弦的构成音，形成音乐上的张力，直到最后又会回归到主和弦将张力释放，这在音乐中叫做（张力的）“解决”。
• 这个过程就像弹簧被拉紧后一放松又会回到最放松的位置，主和弦作为调式中最稳定的和弦，对偏离了主和弦的音有一股吸引力。**各音级与临近的主和弦构成音之间的音程不协和度越高，产生的紧张感就越强，主和弦吸引力就越大。**而和弦进行最终回归主和弦也进一步确认了主音的位置，强化了调性。

旋律方面与和声类似。在经过发展与高潮迭起之后，一个乐句或乐段最终往往会回到主和弦上的音来结束。以主音或主和弦构成音结尾可以使积累起来的张力得到舒缓，在听觉上会给人一种故事讲完了的终止感，尤其是以主音结尾。因此在判断曲调的时候，尤其是设计简单的流行歌，如果没有转调的话，乐段或歌曲的尾音及其最后一个和弦经常能够反应整首歌是什么调的。当然歌曲为了创新求变，例外也有很多。

调性功能与和弦进行

明白了调性音乐的基本逻辑，下面我们就来了解一下各音级与其和弦的调性功能（或和声功能）。由于和弦的功能性主要集中于根音三音五音，而七音与其他引申音起到点缀作用，因此以下内容将以三和弦来分析。

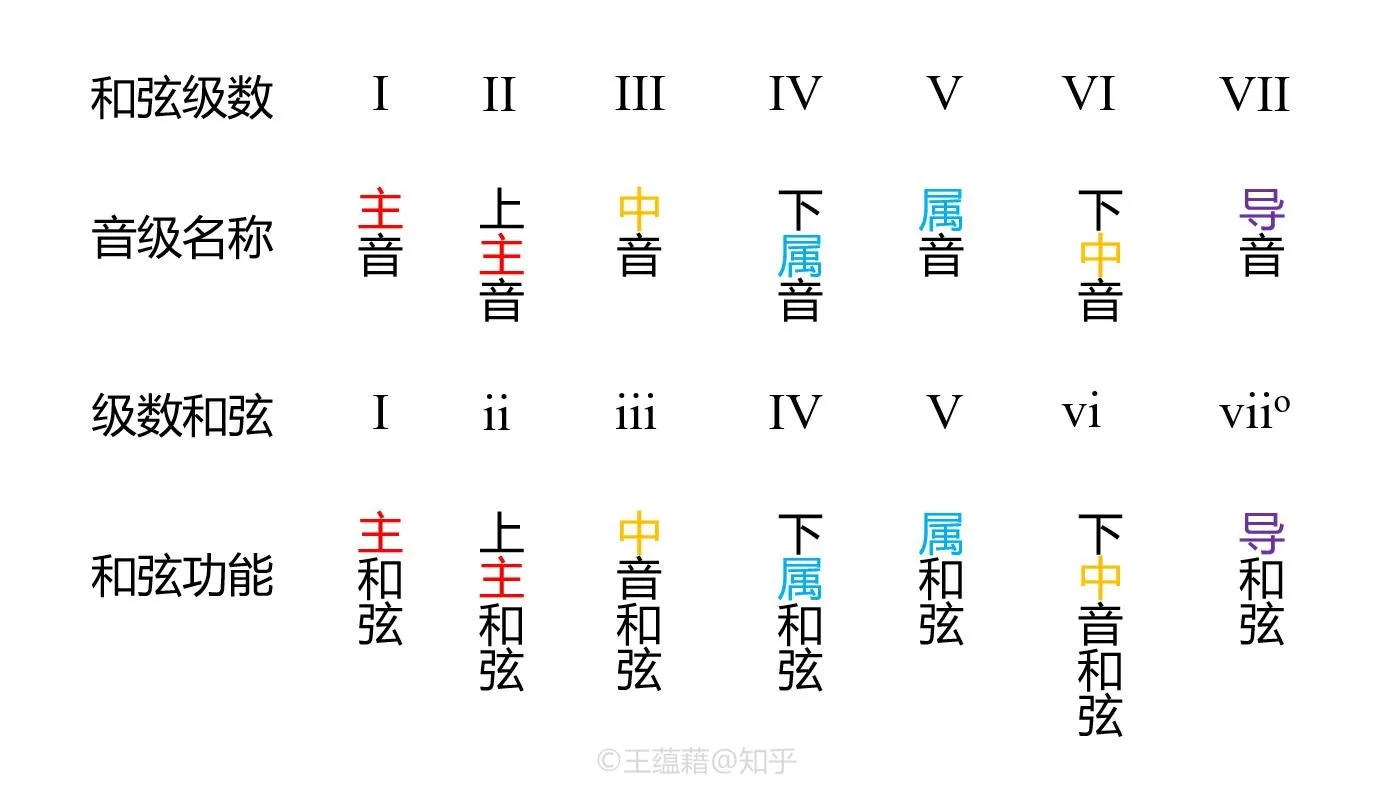
音级类型

大调主和弦的三个构成音 1 3 5 分别叫做主音、中音、属音。主与属是调性音乐中最重要的两个功能音级。而中音夹在两者的正中，与之各相差两个音级，故得名“中音”。由于是主和弦的构成音，主音、中音、属音是调中最稳定的三个音。

以主音为坐标系，音级的命名具有对称性。

• 主音顺阶往上五度的 5 叫做属音，而顺阶往下五度的 4 则叫做下属音；
• 主音顺阶往上三度的 3 叫做中音，而顺阶往下三度的 6 则叫做下中音；
• 主音上方大二度 2 叫做上主音，下方大二度的 b7 叫做下主音（小调中会用到）
• 主音顺阶往下小二度的 7 则叫做导音（顾名思义：把音符引导向主音的那个音）

由此，大调七个音级都拥有了自己的调性功能名称。

下属音与导音分别会与主和弦的一个构成音形成小二度关系，而小二度具有不稳定性，因此这两个非主和弦构成音需要通过半音移动来释放张力。下属音会有往主音中稳定的中音或属音移动的倾向，而导音则明显具有回归主音的强烈倾向。

上主音与下中音既不像主和弦构成音那样稳定，也不像下属音和导音那样需要将张力解决，功能上可以起到过渡的作用。

⭐ 调内和弦的类型

调内和弦也可以用上述调性功能名称来命名：

• I、IV、V 三个大三和弦分别叫做主和弦、下属和弦、属和弦，三者统称为大调的正三和弦。
  • 由于大三和弦音程结构比小三和弦更协和，听起来更明亮，符合大调音乐的气质，因此在大调音乐中正三和弦的使用频率很高。
• ii、iii、vi 三个小三和弦分别叫做上主和弦、中音和弦、下中音和弦，三者统称为大调的副三和弦。
• 减三和弦 viio 则称为导和弦。
  • 导和弦由于减五度很不协和，所以音乐出现的机会最低。

由于七种调性和声功能思考起来太烧脑子，音乐家们根据大调正三和弦的听觉效果把它们归纳为三大类：主功能 T、属功能 D、以及下属功能 S（或属前功能 PD）。

• 主功能和弦包括 I、iii、vi 三个和弦
  • 它们至少含有主和弦中的两个构成音，因此听感上接近主和弦，或像是主和弦的延伸。
• 属功能和弦包括 V 与 viio 两个和弦。
  • 属功能和弦含有大调中最不稳定的导音，而且不含主和弦中的主音与中音，因此最为不稳定，有强烈的回归主和弦的倾向。
  • 另外从音程角度考虑，在属七和弦 V7 与导和弦中下属音 4 与导音 7 还会构成极不协和的三全音，使张力更大，更需要得到解决。
  • iii 虽然也含有导音，但是由于其具有两个主和弦构成音，因此听起来属功能性较弱，它通常被看作是省略了主音的 Imaj7 和弦。
• 下属功能和弦包括 ii 与 IV 两个和弦。
  • 下属功能的和弦含有下属音但不含导音，因此和弦的张力介于主功能和弦与属功能和弦，可以起到从主功能和弦通往属功能和弦的衔接过渡作用。
  • 另外，下属和弦的根音 4 在连接到属和弦的导音 7 时，大脑会感知到不协和并有紧张感的增四度。增四度有强烈扩张到纯五度的倾向，这会加强我们对导音 7 回归主音 1 的期待（经典的 251 走向）。正因为下属功能和弦一般放在属功能和弦的前面，因此也被叫做属前和弦。

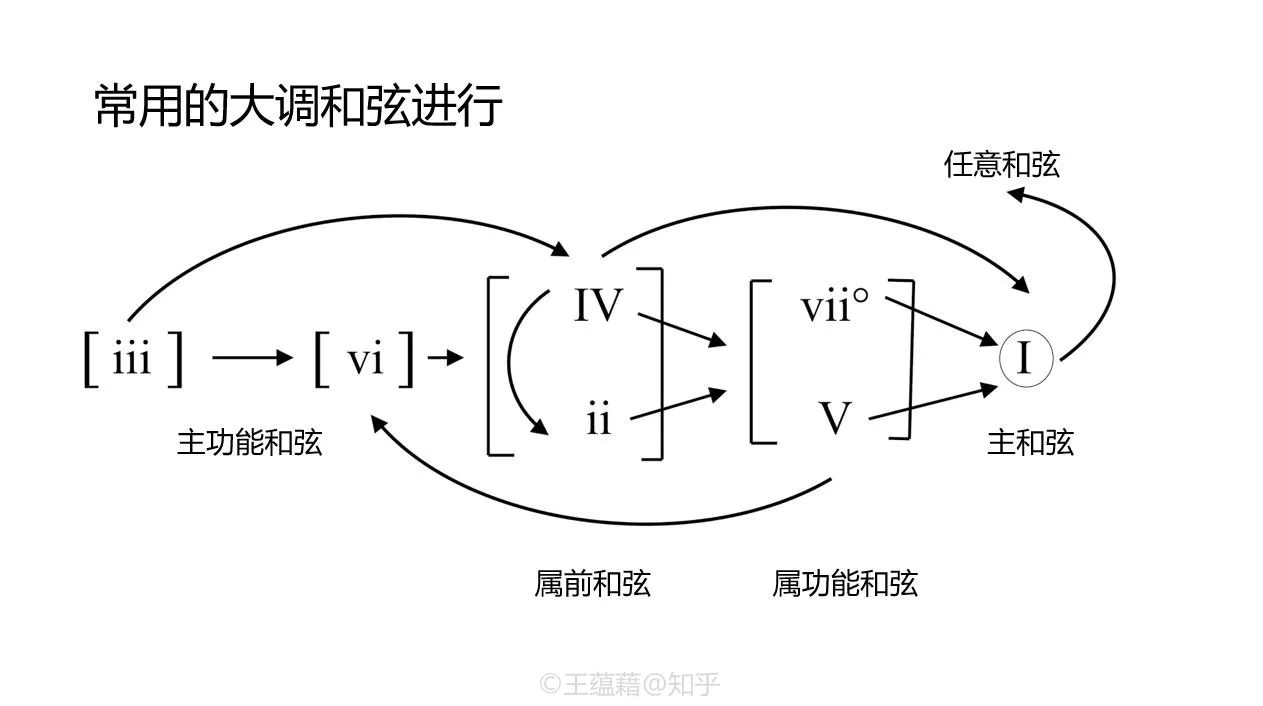
在调性音乐中的和弦进行一般会依照 主 -> 属前 -> 属 -> 主 的先后顺序展开。

• 常见的和弦进行会从主和弦开始，连接到任意一个和弦，并由此进入一个以主和弦为终点的循环。
• 循环中，主功能和弦会首先过渡到属前和弦，然后随着张力的累积进入属功能和弦，最后由属功能和弦回归主功能和弦，并由此结束或进入下一段和弦进行。
• 比如，大调中用烂了的 I-vi-IV-V 进行就符合这个规律，也就是 C 大调中的 C-Am-F-G。
  • 主和弦 I 首先衔接主功能的 vi，接着通过属前和弦 IV 来到属和弦 V，最后回到主和弦 I 形成一个闭环。和弦进行由此可以无限进行下去。

虽然歌曲的和弦进行往往会遵循上述规则顺序，但它并非科玉律，而更多是一种安全的和弦编写的套路参考。满足上述规则顺序的和弦声部连接较为容易，听起来也较为顺畅。但如果偶尔能使用聪明的手法技巧打破常规的和弦进行，或许可以为乐曲带来一番惊喜。

终止式

主音的位置并不是凭空出现的，不存在“神说要有光就有了光”的情况。那主音的位置是如何被确立起来的呢？主音是在和声的推进中确立的。

调性音乐中，最具有确立主音位置以及调性的和声进行就数终止式了。终止式是在乐句、乐段或乐曲结尾处用到的和声安排，即属功能和弦回归主功能和弦的过程，因此它起到张力解决的作用，使乐曲产生终止的听感，故得名“终止式”。

由于属 -> 主的过程中，导音 -> 主音的半音解决突出了主音的位置，因此终止式对建立调性具有重要作用。

乐曲中往往还会将属三和弦 V 改为属七和弦 V7。由于额外增加了一对下属音 -> 中音的半音进行以及一对三全音的解决，属七和弦有助于增强终止式的功能。

终止式一般分为四种：正格终止、半终止、阻碍终止，以及变格终止。

• 正格终止（或完全终止）指的就是属功能和弦到主和弦的终止式，即 V->I（或 viio->I）
  • 由于是真正解决到主和弦，正格终止是最正宗的终止式，也是最强的解决。
• 半终止（或不完全终止）之所以叫半终止，是因为终止式只进行到一半，停在了属和弦 V 上。
  • 停留在属和弦会有一种意犹未尽的感觉，因此半终止感觉就像逗号一样，使乐句稍作停顿后可以继续刚才的内容往下发展。
  • 于此相比，正格终止则像句号一样，可以结束原来的乐句，并开始一个新的乐句。
• 阻碍终止（或伪终止）一般是指将属功能和弦连接到下中音和弦 V -> vi，是假的正格终止式。
  • 当我们听到属和弦时，会期待下一个和弦是主和弦好将乐句终止。
  • 使用下中音和弦则可以将和弦进行从终止式中拉回来继续发展乐句，就像是硬把句子中的句号掰成了逗号的感觉。
  • 由于 vi 可以起到关系小调的主和弦的作用，阻碍终止还具有将乐曲从大调引向关系小调的作用。
• 变格终止（或教堂终止）是由下属和弦接到主和弦的终止式，即 IV-I。
  • 由于没有用到属和弦，变格终止听觉效果上与正格终止非常不同。变格终止的半音移动是由下属音解决回中音，不如导音解决回主音的终止感强，确立主音及调性的能力也更弱。
  • 在教会音乐中，当唱词用到“阿门”来为乐曲结尾时，就会用到变格终止。不过在变格终止之前，往往乐句已经出现过了完全终止，提前将张力释放解决，而变革终止只是起到了结尾的额外延伸。
  • 当然，变格终止并非不能独立使用，比如 Beatles 的《Yesterday》就巧妙地在没有正格终止的帮助下，以变格终止结束了乐曲。

熟悉掌握终止式可以对我们在判断乐曲的调性以及推测乐曲的发展方向时起到非常大的帮助，是必须掌握的内容。

和弦与调式的互生

最后一节，让我们观察一下和弦与调式音阶之间的互生关系，并学习如何跳脱调性思维，改用调式思维来解读音乐。

一方面，和弦源自调式。从第二节中我们观察到，以大调为框架模板可以构建出调内七个音级上的和弦，包括三和弦与七和弦。以 C 大调为例，七个顺阶七和弦分别是 Cmaj7、Dm7、Em7、Fmaj7、G7、Am7，以及 Bø7。

另一方面，和弦又可以构成调式。C 大调这七个和弦可以继续顺着音阶以三度向上堆叠，添加入九度音、十一度音，以及十三度音。它们分别会构成七个顺阶引申和弦：Cmaj13、Dm13、Em11(b9b13)、Fmaj13(#11)、G13、Am11(b13) 和 Bm11(b5b9b13)。

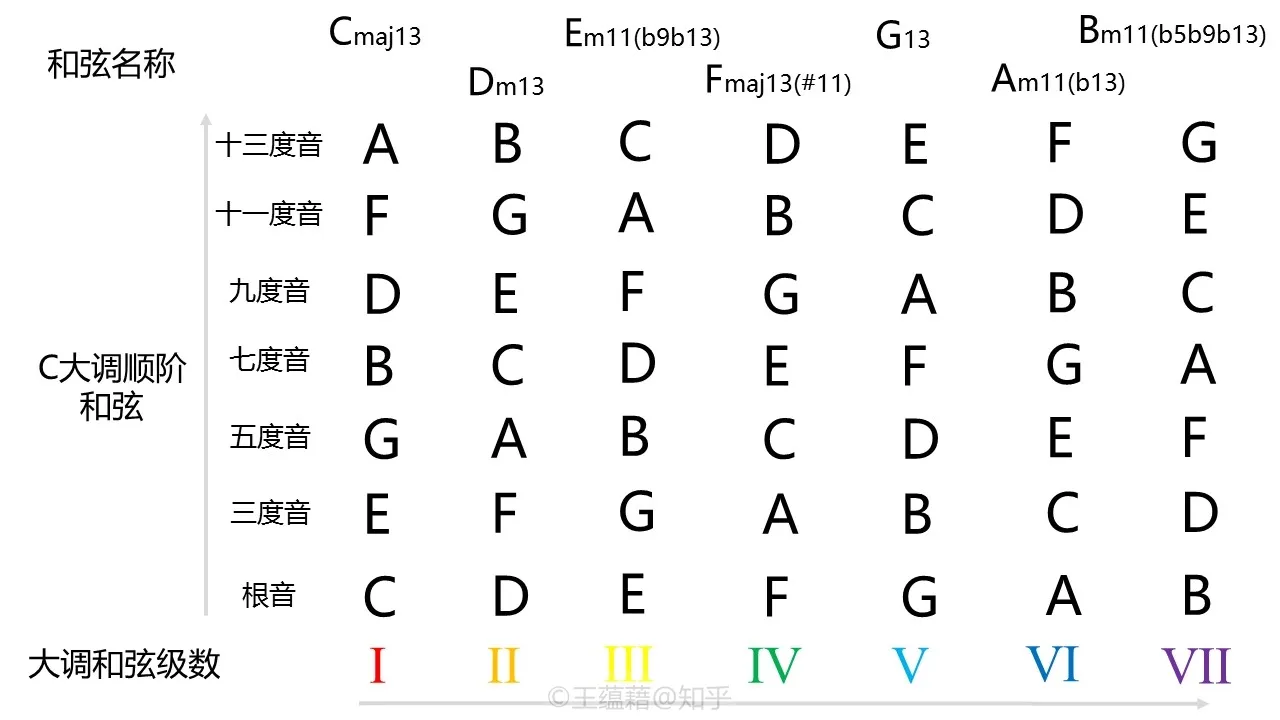
虽然调内三和弦七和弦会存在同属性的和弦，但是引申至十三度的和弦中，没有任何两个和弦类型相同。每一类十三和弦都由根音出发，含有七个组成音，因此和弦自身就构成一条新的音阶。仔细观察可以发现，这七类和弦的音阶分别是自然音阶的七种调式：Ionian、Dorian、Phrygian、Lydian、Mixolydian、Aeolian 和 Locrian。

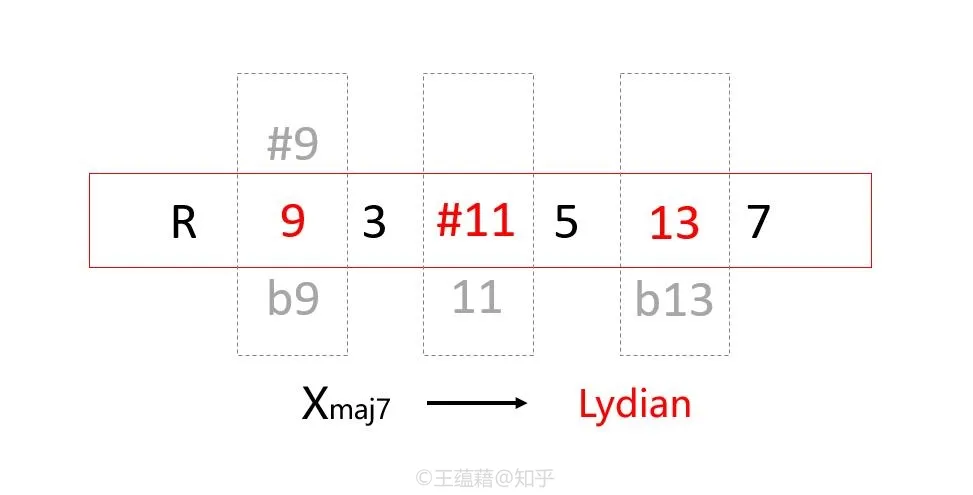
并非只有叠到十三度的引申和弦才可以具有自己的调式音阶，其他和弦照样可以，且自由度更高。在七和弦的四个构成音之外任意插入一个九度音、一个十一度音，以及一个十三度音就可以形成一条调式音阶。

• 比如大七和弦上若选择添加 9、11、13 就构成了 Ionian 调式，而添加 9、#11、13 则构成 Lydian 调式。

虽然任意的添加方式并不能保证音阶协和好听，故并不常用，但理论上我们完全可以选择添加#9、#11、b13 来构成一条类似于匈牙利小调的新调式。

由此，我们完成了一个由调式生和弦，再由和弦生调式的过程。可见，调式与和弦具有互生关系，它们之间并不存在严格的区分线。

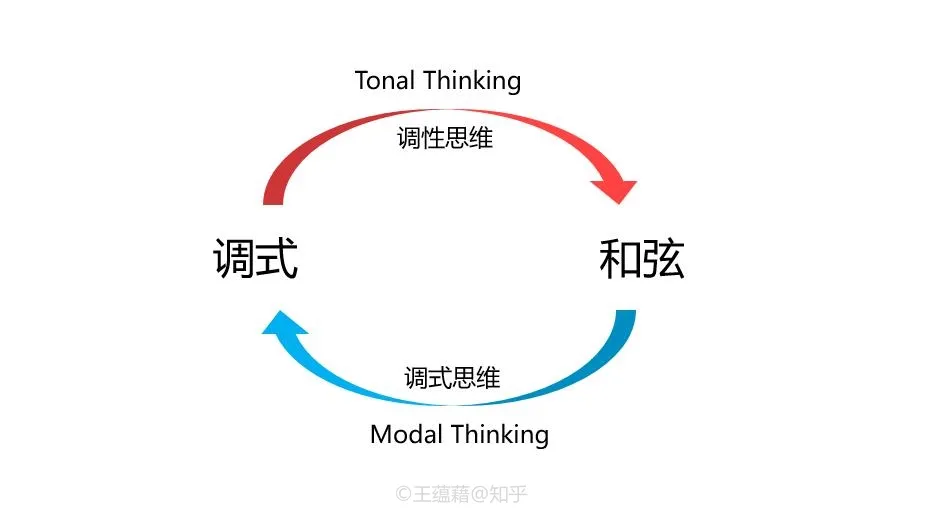
不过，两者所产生的先后顺序体现了两种不同的音乐思维模式。

• 调性思维是以调式生和弦，我们会问：“这个和弦源自什么调式，是由哪个音级中生发出来的？”，这种思维模式适合传统调性音乐的演奏。
• 调式思维则是以和弦生调式，我们会问：“这个和弦可以构成什么样的调式？”，这种思维适合调式音乐，以及含有复杂和弦的调性音乐的演奏。

小调全知道

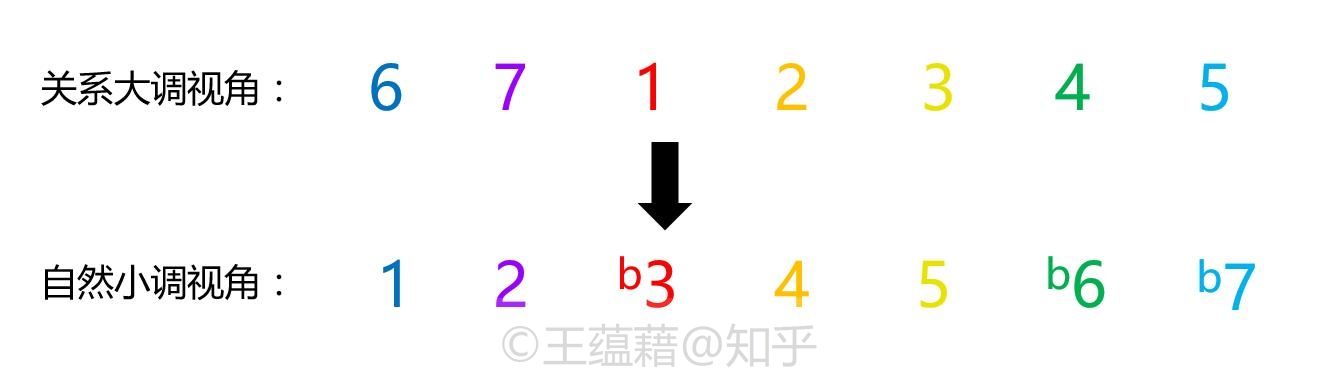
理解小调可以有两种视角：一种是通过关系大调的音阶与和弦来观察小调，一种则是直接从小调主音出发。本文主要提供的是第二种视角。

自然小调与大调的比较

大调开朗活泼，而小调阴沉忧伤。可为什么大小调给人的情感体验会如此不同呢？

首先，从音阶构造来看，自然大调与自然小调音阶中有三个音级是不同的。这三个音级分别是三级、六级、七级。

• 三六七级在大调中与主音分别是大三度、大六度、大七度的关系
• 而在小调中则是小三度、小六度、小七度。
• 小调中唯二的两个半音程出现在了 2 与 b3、以及 5 与 b6 之间。三全音则出现在 2 和 b6 之间。

对习惯了现代音乐的听众来说，小调的三级听起来皆比大调的要来得“含蓄”、“暗沉”、“忧伤”。这我们在比较大三与小三和弦的听感时就已有所体会。

同样的，六度与七度的大小不同，也会影响到情绪。

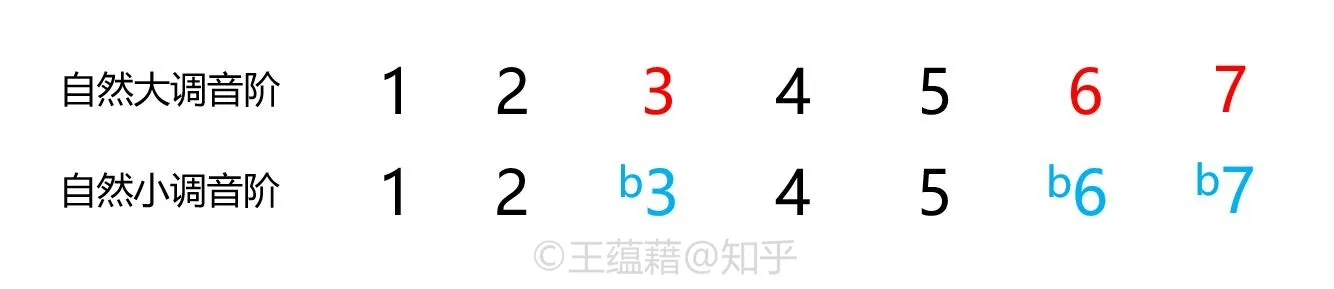
其次，从和弦的角度观察，自然大调里奠定主属功能的一四五级上都是大三和弦，而自然小调的一四五级上则恰好都是小三和弦。而大三和弦则移居到了三六七级上，反而成了相对次要的辅助和弦。

小调二级和弦是比小三和弦还幽暗的减三和弦，若加入七度音则是半减七和弦。半减七的阴沉性格不符合大调的开朗气质，因此不常用；但半减七和弦在小调中非常合适，地位明显得到提升，它是小调中重要的一个属前和弦。

从以上两个角度可以看出，正是由于大调与小调所强调突出的音以及和弦属性不同，造成了它们在情绪色彩上明显的差异。这也是为什么我主张要从小调本身出发学习小调，而不是通过关系大调的推导把小调当大调学。不可否认，关系大调是学习路径上很好的拐杖，但最终我们希望的是能够扔掉拐杖自由行走。

调内顺阶和弦、级数、功能

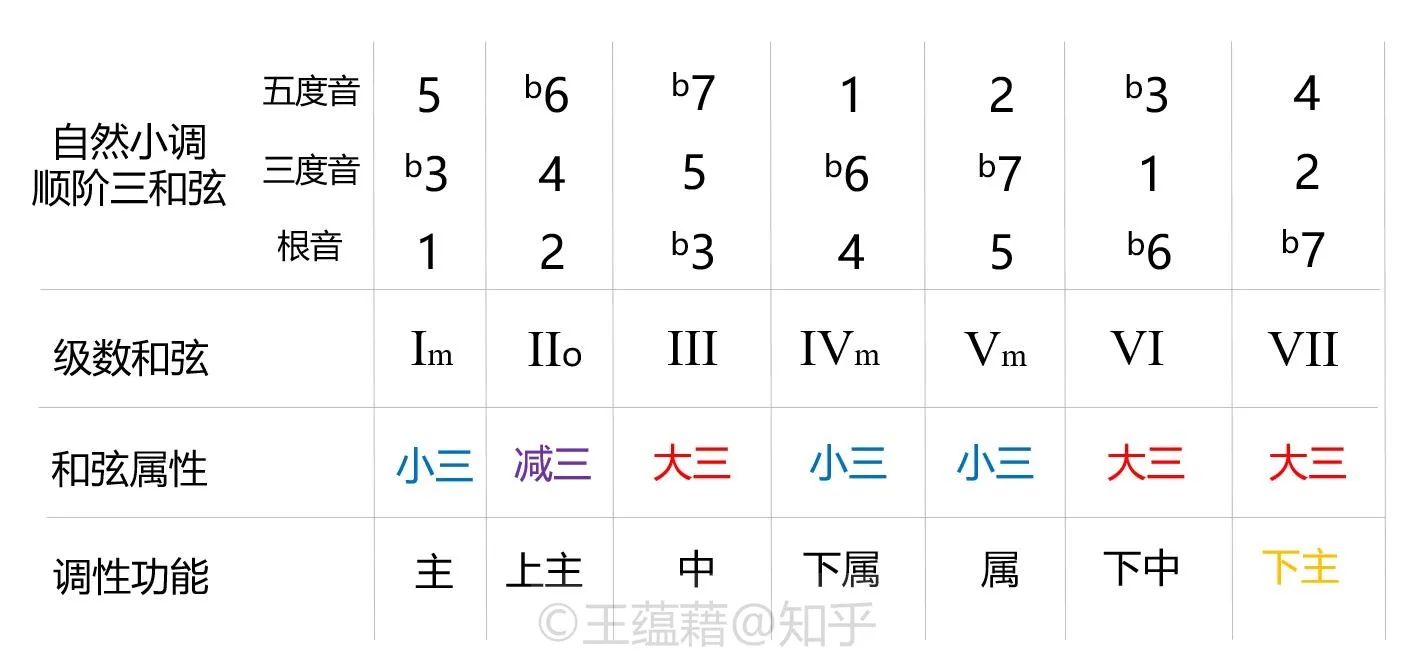
自然小调音级的调性功能与大调基本一致。一到六级分别是主、上主、中、下属、属、下中功能。中音和下中音虽然位置与大调中差了半音，但是功能不变。

然而，自然小调的七级 b7 音却没有资格被叫做导音。导音的定义是主音下方半音程的那个音，即必须是还原 7，而非 b7。不稳定的导音 7 具有能把声部向上半音拉回稳定的主音的功能，而相差全音程的 b7 音则相对稳定不具备导音的作用。故我们改称自然小调的七级为下主音。

顺接三和弦

一四五级是小三和弦，二级是减三，三六七级是大三。

顺接七和弦

七和弦方面，自然小调最重要的一四五级上都是小七和弦，二级是半减七和弦，三六级是大七和弦，而七级是属七和弦。

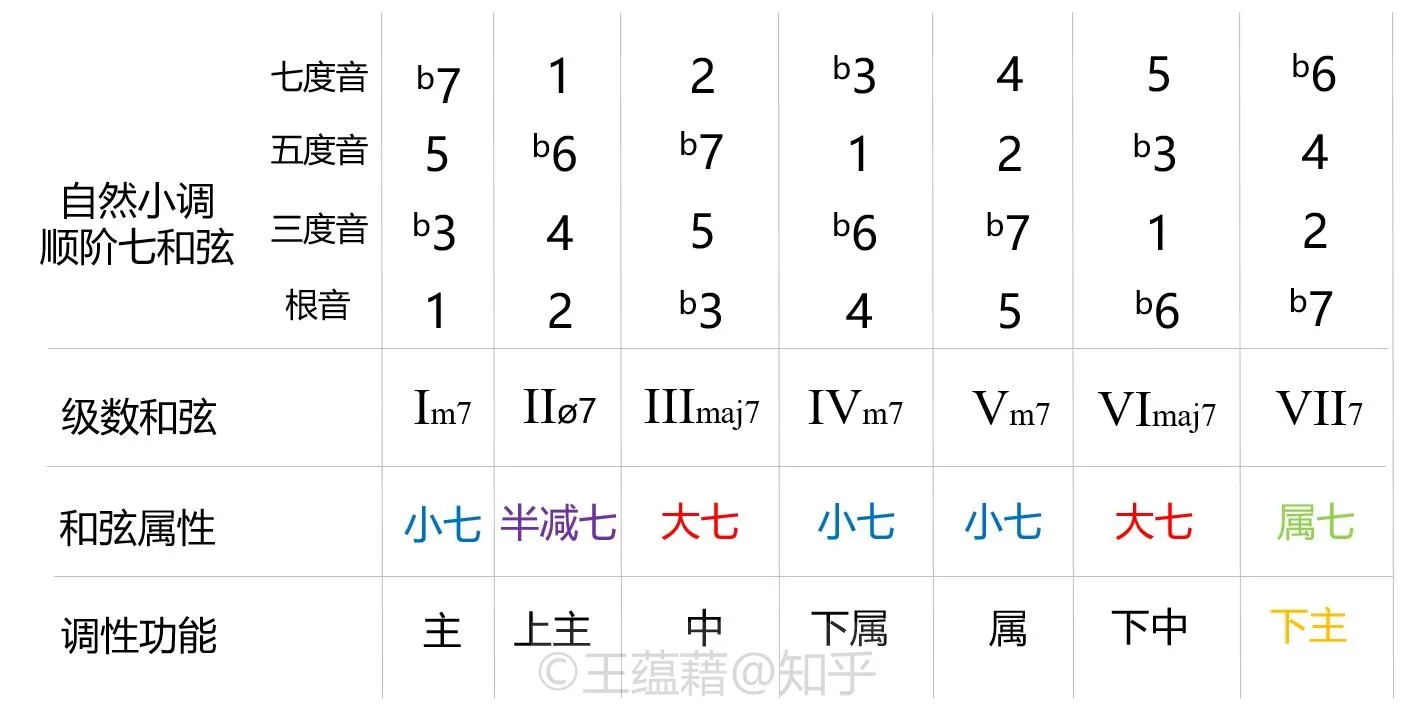
小调和弦的级数标记依然沿用罗马数字，规则与大调的用法基本一样。不过，细心的读者可能已经从图片里发现，在小调三六七级上，虽然根音分别是 b3、b6、b7，但是在级数的标记上则用的是 III、VI、VII，而不是带有降记号的 bIII、bVI、bVII。

事实上，两种标记习惯都是存在的。在古典乐里面，如果乐段默认是小调，小调的调内和弦级数是不带升降号的，根音在 b3、b6、b7 时用 III、VI、VII 标记；而如果出现根音在 3、6、7 音时，则级数分别标记为#III、#VI、#VII。

不过这样的标法是有缺陷的。虽然在调外和弦不多的小调上这样的标记比较干净，但在将来讲到大小调混用时，这样的标记法会造成歧义。因此许多情况下，将大小调的级数标记一视同仁，当根音在 b3、b6、b7 时用 bIII、bVI、bVII 标记，当根音在 3、6、7 时用 III、VI、VII 标记反而是更合理的选择。

至于如何标记，在独自分析时可以根据方便性以及自己的偏好来选择；而在同他人合作时，不论用哪种标记习惯，都应当事先和搭档沟通清楚避免歧义。

⭐ 调内和弦

与学习大调和弦级数时一样，一旦指定了小调的主音位置，我们就可以根据和弦级数快速反应出这个小调所以顺阶和弦的名称。如果将和弦级数套用到 A 自然小调，我们可以得到以下的音阶与调内和弦：

同样，E 自然小调的音阶与调内和弦是：

小调的改良

和声小调

了解了自然小调的基本结构之后，现在我们来思考一下如何在声音上建立小调听感。一来，我们应该相比大调更多地使用具有小调特征的小三和弦。其次，我们可以祭出建立调性时最重要的武器——正格终止式。

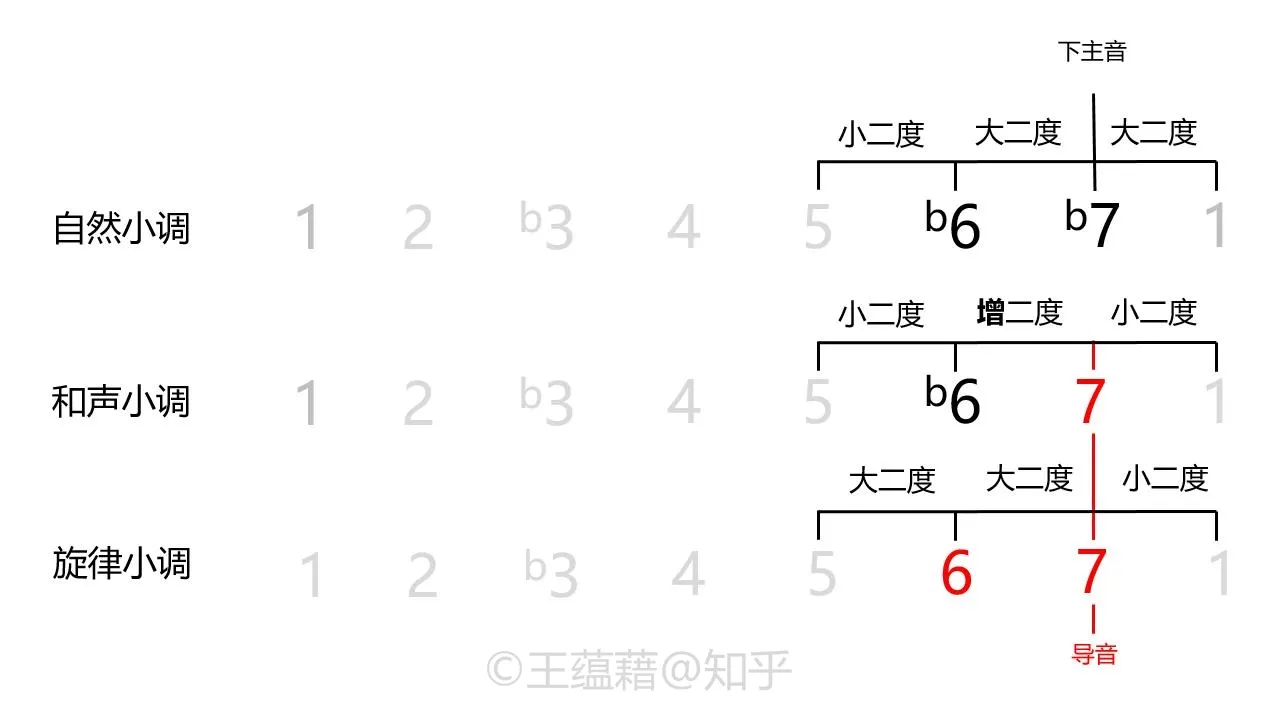
可是，自然小调的正格终止式听起来一点儿也没有“终止”的能力。之前在大调中，V7 和弦的三度音是导音 7，在终止式进行中会向上移动半音到达 I 级和弦的根音，即主音 1 来释放张力。而缺失导音成了自然小调的一个致命缺陷。自然小调的 Vm7 的三度音是下主音 b7,。没有了导音向主音的运动，乐句的终止感、张力的解决感，以及主音的位置都变得暧昧不清。这么说来，自然小调本身调性是不稳定的，歌曲可能放着放着就听偏到关系大调去了。

音乐家们当然不会对这么巨大的 Bug 置之不理！为了保障小调调性的独立与稳定性，音乐家们为小调打下了第一款补丁——和声小调。“一号补丁”规定：

1. 一般情况下，小调按照自然小调规则照常运行。
2. 当小调的和声进行到属功能和弦时，我们将放弃自然小调的下主音，改用导音作为小调音阶的七级音。
3. 当小调和声从属功能返回主功能时，则将七级音回归到下主音。

而在上述属功能状态下，具有升高了半音的七度音的临时小调就叫做和声小调，它的音阶由 1 2 b3 4 5 b6 7 1 构成。

和声小调弥补了自然小调在属功能上的弱势。通过引入导音，我们使小调的 V 级和弦由自然小调中的小七和弦转变为了和声小调中的属七和弦，大大提升了终止式的效果。

旋律小调

不过，“一号补丁”也带来了一个奇特的副作用，或者说是新的 bug：由于七度音的提高，和声小调的六度音 b6 与七度音 7 构成了一个增二度音程。增二度音程听感很特别，满满的异域风情与小调原本想表达的忧伤感受很不一样，而用到了和声小调的歌曲往往会被描述成具有阿拉伯或西班牙音乐的感觉。一旦使用不慎的话，歌曲会带有浓重中东烤串儿味道。

于是，为了弥补新出现的小 bug，音乐家们出台了小调的第二款补丁——旋律小调。“二号补丁”规定：

1. 一般情况下，小调按照自然小调规则照常运行。
2. 当小调的和声进行到属功能和弦时，我们将把音阶中的六度和七度音各自提升半音。
3. 当小调和声从属功能返回主功能时，则将六级和七级音各降半音，还原回自然小调音阶。

举例来讲：前一张图片中小调的 IIø->V7->Im 进行中，属前功能的 IIø 来自自然小调，当音乐进入属功能时，小调将切换到旋律或和声小调，形成 V7 和弦，而非 Vm7 和弦。当音乐由属功能返回主功能时，小调又会切换回自然小调，构成 Im7 和弦。

“二号补丁”在和声小调提升七度音来构建属和弦的基础上，又同时提升了六度音，形成旋律小调音阶：1 2 b3 4 5 6 7 1。提升了六音和七音后，旋律小调既解决了自然小调属功能中缺乏导音没法终止的缺陷，又化解了和声小调里增二度听感诡异的尴尬。拥有了终止式，小调的调性也就明朗了。经过改良后的小调终于可以和大调平起平坐了。完美~

综上说述，当我们谈论“小调”时，我们一般指的是安装了“一号”和“二号补丁”的小调。它既不是自然小调，也不是和声小调或旋律小调，而是随着属主功能变化而游走于三者之间的结合体。是三种小调式共同塑造了小调的听感。不过，这也不妨碍我们把小调拆解成三种调式来分别研究。上文已经研究过了自然小调的结构，下面我们就来观察一下和声小调与旋律小调的结构（初学者可以跳过这节内容）。

和声小调与旋律小调的结构

自然大调与自然小调虽然音级结构不同，但是它们归根结底还是衍生自同一音阶类型：自然音阶。然而，和声小调和旋律小调却来自另外两种音阶类型。因此，和声小调与旋律小调中的顺阶和弦也必然与自然音阶中的结构有所不同。

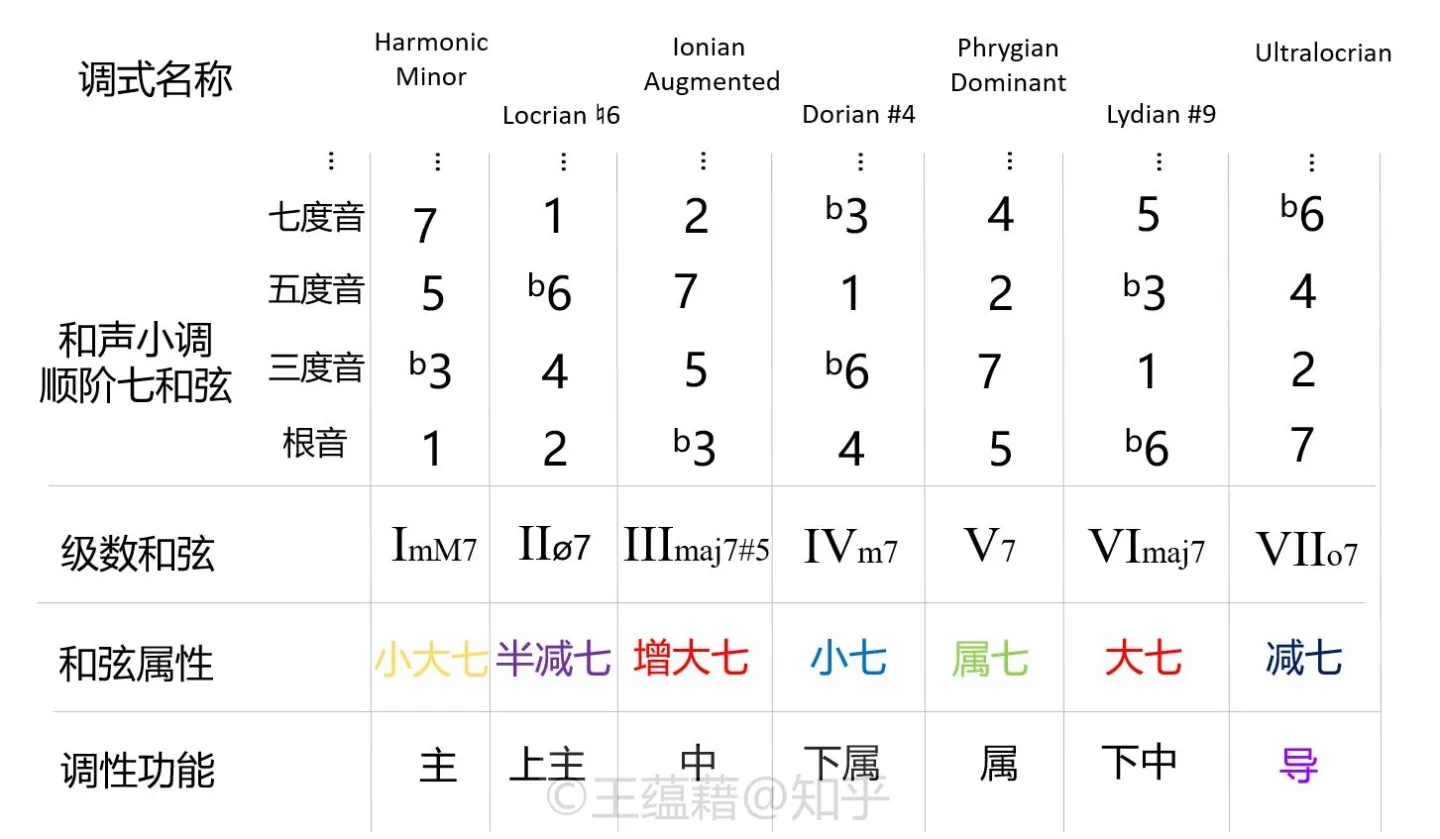
首先，我们观察一下和声小调。和声小调音阶是 1 2 b3 4 5 b6 7 1，形成的顺阶七和弦属性依次为：小大七、半减七、增大七、小七、属七、大七、减七。扩展至顺阶十三和弦与它们衍生出的调式分别是：

• I 级十三和弦：ImM7(9,11,b13)，形成 Harmonic Minor 调式（和声小调本身）
• II 级十三和弦：IIø7(b9,11,13)，形成 Locrian ♮6 调式；
• III 级十三和弦：III+maj7(9,11,13)，形成 Ionian Augmented 调式；
• IV 级十三和弦：IVm7(9,#11,13)，形成 Dorian #4 调式；
• V 级十三和弦：V7(b9,11,b13)，形成 Phrygian Dominant（Phrygian Major）调式；
• VI 级十三和弦：VImaj7(#9,#11,13)，形成 Lydian #9 调式；
• VII 级十三和弦：VIIo7(b9,b11,b13)，形成 Ultralocrian 调式。

这些和弦结构和名字看着可能很陌生很复杂，但是有一个好消息：这七组和弦与调式中，只有一组是非常值得关注的，那就是起到了属功能的 V 级了。和声小调之所以存在正是为了满足属功能的需求。

和声小调的属和弦和大调结构并不相同。大调的属和弦 V9(13) 的引申音是 9,13，而和声小调的属和弦 V7(b9,b13) 引申音却是 b9,b13。（十一度音是 V7 和弦的避免音，往往不会用，或者得在没有三度的 V7sus4 作为四度音使用。在此可以忽略。）V7(b9,b13) 和弦的 b9、b13 音虽然带有变音记号，但是这两个音分别是小调中的 b6 和 b3，都是调内音，因此 V7(b9,b13) 和弦是小调天然的属和弦。

这给音乐家们一个启示：属和弦并非只能来自一种音阶，也并非只能衍生出一种音阶。九度与十三度这两个引申音的选择会决定一个属和弦听起来更具大调的明亮感，还是更有小调的忧伤感——或者甚至可以是两者的混搭（我们下面就会看到）。

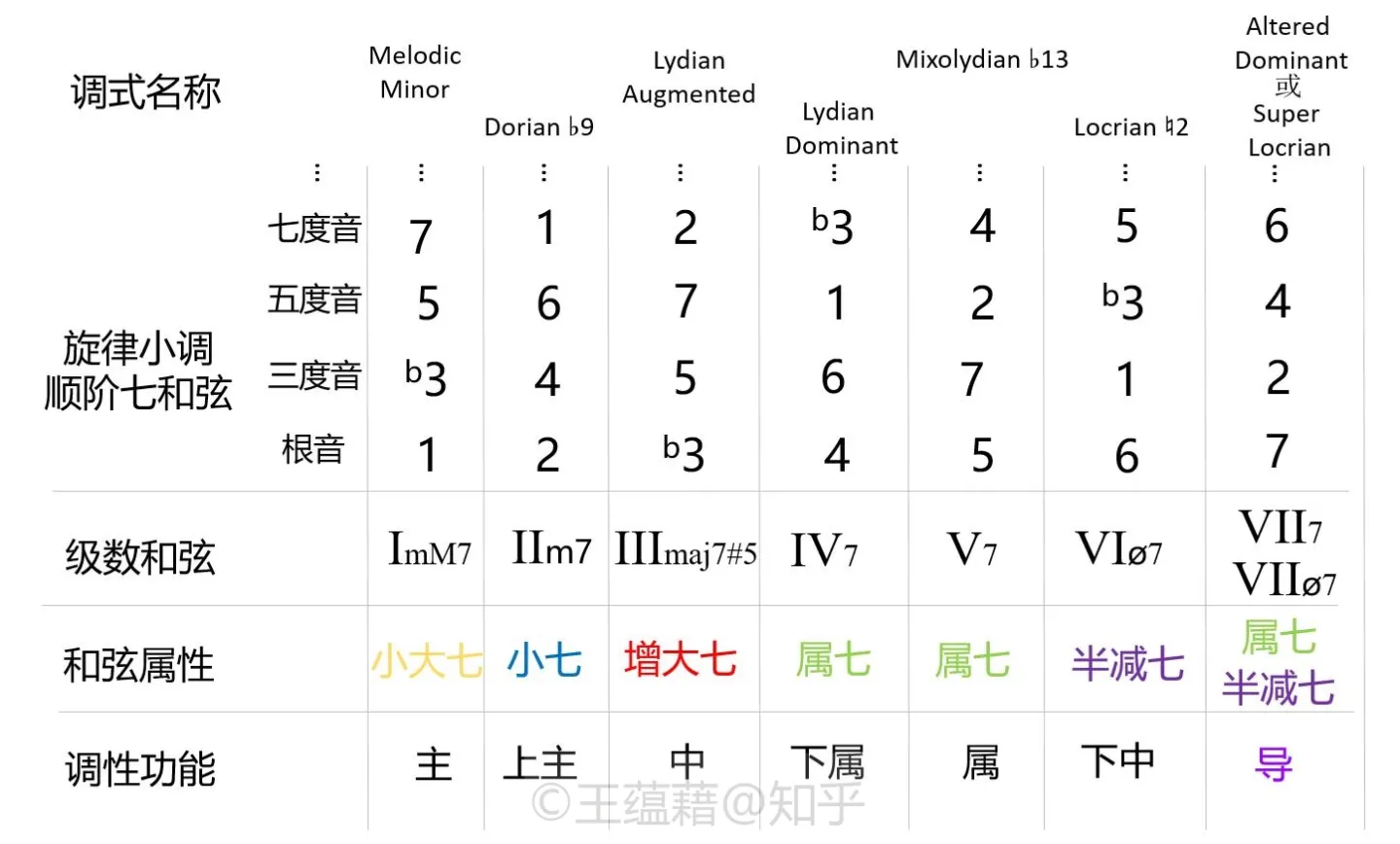
接着，我们观察一下旋律小调。旋律小调音阶是 1 2 b3 4 5 6 7 1，形成的顺阶七和弦属性依次为：小大七、小七、增大七、属七、属七、半减七、属七（或半减七）。扩展至顺阶十三和弦与它们衍生出的调式分别是：

• I 级十三和弦：ImM7(9,11,13)，形成 Melodic Minor 调式 (旋律小调本身）；
• II 级十三和弦：IIm7(b9,11,13)，形成 Dorian b9 调式；
• III 级十三和弦：III+maj7(9,#11,13)，形成 Lydian Augmented 调式；
• IV 级十三和弦：IV7(9,#11,13)，形成 Lydian Dominant (Mixolydian #11) 调式；
• V 级十三和弦：V7(9,11,b13)，形成 Mixolydian b13 调式；
• VI 级十三和弦：VIø7(9,#11,13)，形成 Locrian ♮9 调式；
• VII 级十三和弦：VIIø7(b9,b11,b13)，形成 Superlocrian 调式：1 b2 b3 b4 b5 b6 b7 1；或 VII7(b9,#9,b5,#5)，形成 Altered Dominant 调式：1 b9 #9 3 b5 #5 b7 1。由于异名同音的关系，这个调式和弦类型可以有两种解释，既可以是半减七又可以是属七和弦。

旋律小调竟然同时有三种不同类型的属七和弦：四级上的 13#11 和弦、五级上的 9(b13) 和弦，以及七级上的 7(b9,#9,b5,#5) 和弦。其中 7(b9,#9,b5,#5) 也叫变化属七和弦，简写为 7alt，它是包含了所有可能的变化音级的属和弦。.注意，在 7alt 和弦中#11 与 b5 其实是同一个音，b13 与#5 也是同一个音，两种标记方式都行得通。

以上变化和弦结构都可以拿来套用到大小调五级上，代替天然的属和弦结构。虽然这会添加调外音进来，但由于属和弦本身目的就是积累张力，将音乐的剧情引入高潮，音乐家在实践中发现替换属和弦的效果非常好，往往可以带来惊艳的听觉刺激。当然也有一个例外，那就是大调天然的 V9(13) 如果引入小调，会让小调突然丢失原有的忧伤紧张感，效果很不佳，应该避免。

除了属和弦，旋律小调与和声小调中另外值得一提的是的一级和弦。ImM7 是一个非常不稳定的结构，和声听感很不协和，因此不适合当做主和弦。即使把 7 音替换为 6 音形成 Im6，和弦依旧具有很高的不协和性。也就是说和声小调和旋律小调在传统调性和声中是无法独立存在的，因此它只能被用作自然小调的一个“补丁包”、“扩展包”。当然，现代音乐早已打破了这些限制，让和声或旋律小调获得了更多自主性，听众的耳朵也越来越适应不协和的和声色彩了。比如在爵士乐中，旋律小调不再被看做是自然小调的附庸，而是独立的存在，并被冠名为的“爵士小调”。

篇幅原因，和声小调与旋律小调的内容我只能暂时点到为止了。若想彻底掌握以上两种类型的音阶，在这方面成为大师，大家必须花出至少同学习自然大小调一样的时间精力来理解记忆才行。

Dorian 小调

在学习区分不同的小调时，除了自然、和声小调、旋律小调之外，人们有时会把 Dorian 小调也拿来比较。

“Dorian 小调” 其实就是 Dorian 调式：1 2 b3 4 5 6 b7 1。因为 Dorian 也具有小调的 b3 度音，而且与自然小调非常相似，只有在六度音这一处地方不同，故被拿来当作比较。这也是为什么 Dorian 会被叫作一种 “小调”。Dorian 调式的六度音是 6，与旋律小调相同，与自然小调及和声小调不同；而 Dorian 调式的七度音则与自然小调相同，与旋律小调及和声小调的不同。

Dorian 调式本来并非是调性音乐的概念，而是调式音乐中的术语。但是我们可以把 Dorian 调式看作是针对自然小调的一款特殊补丁。由于没有导音，所以不同于和声与旋律小调这两个“补丁包”，Dorian 调式并没有修改调性功能的能力。不过，它允许我们在不引入导音的情况下，在旋律中把自然小调的 b6 音替换为 6，造成 Dorian 调式独特的色彩。我们姑且称它为自然小调的 “Mod 补丁” 吧。

我们其实可以依样画葫芦，在小调中安装 Phrygian 调式甚至是 Locrian 的 “Mod 补丁” 让和声色彩变得灰暗，或者大调中临时借用到 Lydian 或 Mixolydian 调式，让音乐瞬间带有遨游仙境的梦幻感或是抽着雪茄烟葛优躺的懒散感。