技巧
输入输出
笔试可能会遇到牛客网 ACM 模式的题目,所以要熟悉一下各种语言的输入输出
Golang
基本格式
基本写法:用一个 for 循环包着,用 Scan 函数接收用空白分隔符分开来的参数。
package main
import "fmt"
func main() {
var a, b int
for {
// 循环获取输入
if _, err := fmt.Scan(&a, &b); err == nil {
fmt.Println(a + b)
} else {
break
}
}
}
另一种写法,判断 err 是否是 io.EOF 类型
package main
import (
"fmt"
"io"
)
func main() {
var a, b int
for {
if _, err := fmt.Scan(&a,&b); err != io.EOF {
fmt.Println(a + b)
} else {
break
}
}
}
包含输入个数
如果题目提供了输入参数的个数 t,那就在循环外提前接收:
package main
import "fmt"
func main() {
var t, a, b int
fmt.Scan(&t) // 返回的参数都省略掉了
for t > 0 {
fmt.Scan(&a, &b)
fmt.Println(a + b)
t--
}
}
包含退出条件
如果题目提供了退出的条件,也不用接受 io.EOF 了,在循环内判断退出条件即可:
package main
import "fmt"
func main() {
var a, b int
for {
fmt.Scan(&a, &b)
if a == 0 && b == 0 {
// 退出条件就是两者均为0
break
}
fmt.Println(a + b)
}
}
不固定参数个数
如果题目的一行输入个数是不固定的,并且每行第一个数代表了参数个数:
package main
import "fmt"
func main() {
var n, num int
for {
fmt.Scan(&n) // 先取每行第一个数,确定个数
if n == 0 {
// 退出条件,总会给你的
break
}
sum := 0
for n > 0 {
// 再套个循环,写真正的业务逻辑
fmt.Scan(&num)
sum += num
n--
}
fmt.Println(sum)
}
}
这种情况还可以用 bufio 来做:
package main
import (
"fmt"
"os"
"bufio"
"strings"
"strconv"
)
func main() {
input := bufio.NewScanner(os.Stdin) // 创建并返回一个从os.Stdin读取数据的Scanner
for input.Scan(){
// Scan方法获取当前位置的token(该token可以通过Bytes或Text方法获得),
// 并让Scanner的扫描位置移动到下一个token。
// 当扫描因为抵达输入流结尾或者遇到错误而停止时,本方法会返回false
nums := strings.Split(input.Text(), " ") // 分割字符串
if nums[0] == "0" { // 判断是否结束
break
}
res := 0
for i := 1; i < len(nums); i++ {
num, _ := strconv.Atoi(nums[i]) // 字符串转数字
res += num
}
fmt.Println(res)
}
}
这种方法比较麻烦。。。在接收字符串类型的情况时会比较好用
有时候不会给你退出条件,而是在开头提供了行数:
package main
import (
"fmt"
)
func main() {
var t, n, num int
fmt.Scan(&t)
for ; t > 0; t-- {
fmt.Scan(&n)
res := 0
for ; n > 0; n-- {
fmt.Scan(&num)
res += num
}
fmt.Println(res)
}
}
不固定参数个数,且不提供个数
只能用 bufio 了。。。
package main
import (
"bufio"
"fmt"
"os"
"strconv"
"strings"
)
func main() {
input := bufio.NewScanner(os.Stdin)
for input.Scan() {
nums := strings.Split(input.Text(), " ")
if len(nums) == 0 {
break
}
res := 0
for _, num := range nums {
tmp, _ := strconv.Atoi(num)
res += tmp
}
fmt.Println(res)
}
}
希望这种题远离我
Python
nums = list(map(int, input().split()))
数组
双指针
计算过程仅与两端点相关的称为双指针。
这种方法通过一个快指针和慢指针在一个 for 循环下完成两个 for 循环的工作。
- 快慢指针:都从头开始,遍历条件不同,所以速度不同
- 头尾指针:一个从头,一个从尾;二分法就是一种头尾指针;也叫对撞指针
题目
头尾指针:[offer 57](array\剑指 Offer 57. 和为 s 的两个数字.md)
快慢指针:
滑动窗口
计算过程与两端点表示的区间相关的称为滑动窗口。
滑动窗口本身并不是解决问题的一种方法(或者说算法),它其实就是问题本身。
滑动窗口一定是同向移动的。
�一些经验之谈
- while 循环的条件一般都是
j<len(nums)(右边界不超出) - while 循环内的 j 不断右移;如果 j 右移到一定程度满足了题目的要求后,i 开始右移(一般在 while 循环里的嵌套 while 中运行)
- 滑动窗口给我一种蠕动的感觉。。。
- 有时候为了方便,i 会是左边界左一位,从 -1 开始;j 会是右边界右一位,从 1 开始
二分
时间复杂度:O(logN)
二分搜索有 4 大基础变种题:
- 查找第一个值等于给定值的元素
- 查找最后一个值等于给定值的元素
- 查找第一个大于等于给定值的元素
- 查找最后一个小于等于给定值的元素
package leetcode
// 二分查找第一个与 target 相等的元素,时间复杂度 O(logn)
func searchFirstEqualElement(nums []int, target int) int {
low, high := 0, len(nums)-1
for low <= high {
mid := low + (high - low) >> 1 // or (low + high) >> 1
if nums[mid] > target {
high = mid - 1
} else if nums[mid] < target {
low = mid + 1
} else {
if (mid == 0) || (nums[mid-1] != target) {
// 找到第一个与 target 相等的元素
return mid
}
high = mid - 1
}
}
return -1
}
// 二分查找最后一个与 target 相等的元素,时间复杂度 O(logn)
func searchLastEqualElement(nums []int, target int) int {
low, high := 0, len(nums)-1
for low <= high {
mid := low + ((high - low) >> 1)
if nums[mid] > target {
high = mid - 1
} else if nums[mid] < target {
low = mid + 1
} else {
if (mid == len(nums)-1) || (nums[mid+1] != target) {
// 找到最后一个与 target 相等的元素
return mid
}
low = mid + 1
}
}
return -1
}
// 二分查找第一个大于等于 target 的元素,时间复杂度 O(logn)
func searchFirstGreaterElement(nums []int, target int) int {
low, high := 0, len(nums)-1
for low <= high {
mid := low + ((high - low) >> 1)
if nums[mid] >= target {
if (mid == 0) || (nums[mid-1] < target) {
// 找到第一个大于等于 target 的元素
return mid
}
high = mid - 1
} else {
low = mid + 1
}
}
return -1
}
// 二分查找最后一个小于等于 target 的元素,时间复杂度 O(logn)
func searchLastLessElement(nums []int, target int) int {
low, high := 0, len(nums)-1
for low <= high {
mid := low + ((high - low) >> 1)
if nums[mid] <= target {
if (mid == len(nums)-1) || (nums[mid+1] > target) {
// 找到最后一个小于等于 target 的元素
return mid
}
low = mid + 1
} else {
high = mid - 1
}
}
return -1
}
模拟行为
这类题目不怎么涉及到算法,就是纯粹的模拟行为。。。
单调栈
单调栈的作用是:用 O(n) 的时间得知所有位置两边第一个比他大 (或小) 的数的位置。
最经典的就是接雨水了
链表
链表他妈的就是双指针!!!
有时候递归也可以
虚拟头节点是一个很好的东西
- 链表的一大问题就是操作当前节点必须要找前一个节点才能操作。这就造成了,头结点的尴尬,因为头结点没有前一个节点了。
- 每次对应头结点的情况都要单独处理,所以使用虚拟头结点的技巧,就可以解决这个问题
反向遍历节点
function print_values_in_reverse(ListNode head)
if head is NOT null
print_values_in_reverse(head.next)
print head.val
栈
匹配问题都是栈的强项
字符串
KMP
多复习……
// strStr KMP算法 时间复杂度O(N+M),空间复杂度O(M)
func strStrSimple(haystack string, needle string) int {
n, m := len(haystack), len(needle)
if m == 0 {
return 0
}
next := make([]int, m)
GetNext(next, needle)
// 因为next数组里记录的起始位置为0
j := 0
// i从0开始匹配
for i := 0; i < n; i++ {
// 如果不匹配,就寻找之前匹配的位置
for j > 0 && haystack[i] != needle[j] {
j = next[j-1]
}
// 如果匹配,i和j同时向后移动
if haystack[i] == needle[j] {
j++
}
// 如果j从0移动到m的位置,意味着模式串needle与文本串haystack匹配成功
if j == m {
return i - m + 1
}
}
return -1
}
func GetNext(next []int, s string) {
// next[j]就是记录着j(包括j)之前的子串的相同前后缀的长度。
j := 0
next[0] = 0
// j指向前缀起始位置,i指向后缀起始位置
for i := 1; i < len(s); i++ {
// 如果前后缀不相同,那么j就要向前回退
for j > 0 && s[i] != s[j] {
j = next[j-1]
}
// 说明找到了相同的前后缀, j++,同时记录next[i]
if s[i] == s[j] {
j++
}
next[i] = j
}
}
哈希表
遇到字符串问题,而且字符范围都是小写/大写字母的时候,可以用 [26]int32 来代替一个 map[byte]int32
树
二叉树的遍历
先序遍历
最简单
- 初始头节点入栈
- 每次从栈中取一个节点,打印之,再把它的右节点、左节点先后入栈
// 非递归
func inorderTraversal(root *TreeNode) []int {
if root == nil {
return []int{}
}
res := make([]int,0)
stack := []*TreeNode{root}
var curNode *TreeNode
for len(stack) != 0 {
curNode = stack[len(stack)-1]
stack = stack[:len(stack)-1]
if curNode.Right != nil{
stack = append(stack, curNode.Right)
}
res = append(res, curNode.Val)
if curNode.Left != nil{
stack = append(stack, curNode.Left)
}
}
return res
}
后序遍历
跟先序很像,相当于反着的先序
区别:
- 从栈中取出的节点放进一个数组中;最后数组反着输出
- 入栈顺序是先右�后左
// 非递归
func postorderTraversal(root *TreeNode) []int {
if root == nil {
return []int{}
}
result := make([]int, 0)
stack := list.New()
stack.PushBack(root)
var curNode *TreeNode
for stack.Len() != 0 {
curNode = stack.Back().Value.(*TreeNode)
stack.Remove(stack.Back())
result = append([]int{curNode.Val}, result...) // 将结果放在最前面
// 入栈顺序先左后右
if curNode.Left != nil {
stack.PushBack(curNode.Left)
}
if curNode.Right != nil {
stack.PushBack(curNode.Right)
}
}
return result
}
// 非递归2
func postorderTraversal(root *TreeNode) []int {
if root == nil {
return []int{}
}
result := make([]int, 0)
stack := list.New()
stack.PushBack(root)
var curNode *TreeNode
for stack.Len() != 0 {
curNode = stack.Back().Value.(*TreeNode)
stack.Remove(stack.Back())
result = append(result, curNode.Val)
// 入栈顺序先左后右
if curNode.Left != nil {
stack.PushBack(curNode.Left)
}
if curNode.Right != nil {
stack.PushBack(curNode.Right)
}
}
reverse := func(nums []int) []int {
i, j := 0, len(nums)-1
for i < j {
nums[i], nums[j] = nums[j], nums[i]
i++
j--
}
return nums
}
return reverse(result) // 反转
}
中序遍历
相对难一点,在使用迭代法写中序遍历时,就需要借用指针的遍历来帮助访问节点,栈则用来处理节点上的元素。
- cur 指向根节点
- cur 一直左移,一直将 cur 的左节点入栈,直到左节点为空
- 若左节点为空,出栈并赋值为 cur,打印;cur 转到其右节点,再重复步骤 2
func inorderTraversal(root *TreeNode) []int {
if root == nil {
return []int{}
}
stack := list.New()
result := make([]int, 0)
curNode := root // 指针
for stack.Len() != 0 || curNode != nil { // 注意这里的条件!
if curNode != nil {
stack.PushBack(curNode)
curNode = curNode.Left
} else {
// 左边没有了
curNode = stack.Back().Value.(*TreeNode) // 出栈
stack.Remove(stack.Back())
result = append(result, curNode.Val) // 打印
curNode = curNode.Right
}
}
return result
}
回溯
回溯是递归的副产品,只要有递归就会有回溯。
虽然回溯法很难,很不好理解,但是回溯法并不是什么高效的算法。因为回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。
回溯法解决的问题都可以抽象为树形结构。因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度构成了树的深度。
问题分类
- 组合问题:N 个数里面按一定规则找出 k 个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个 N 个数的集合里有多少符合条件的子集
- 排列问题:N 个数按一定规则全排列,有几种排列方式
- 棋盘问题:N 皇后,解数独等等
组合不强调元素顺序的,排列强调元素顺序
模板
回溯函数模板返回值以及参数
习惯性将函数起名为 backtracking
回溯算法中函数一般无返回值
再来看一下参数,因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来,所以一般是先写逻辑,然后需要什么参数,就填什么参数。
回溯函数伪代码如下:
void backtracking(参数)
回溯函数终止条件
遍历树形结构一定要有终止条件,所以回溯也有要终止条件。
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
所以回溯函数终止条件伪代码如下:
if (终止条件) {
存放结果;
return;
}
回溯搜索的遍历过程
在上面我们提到了,回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。
如图:
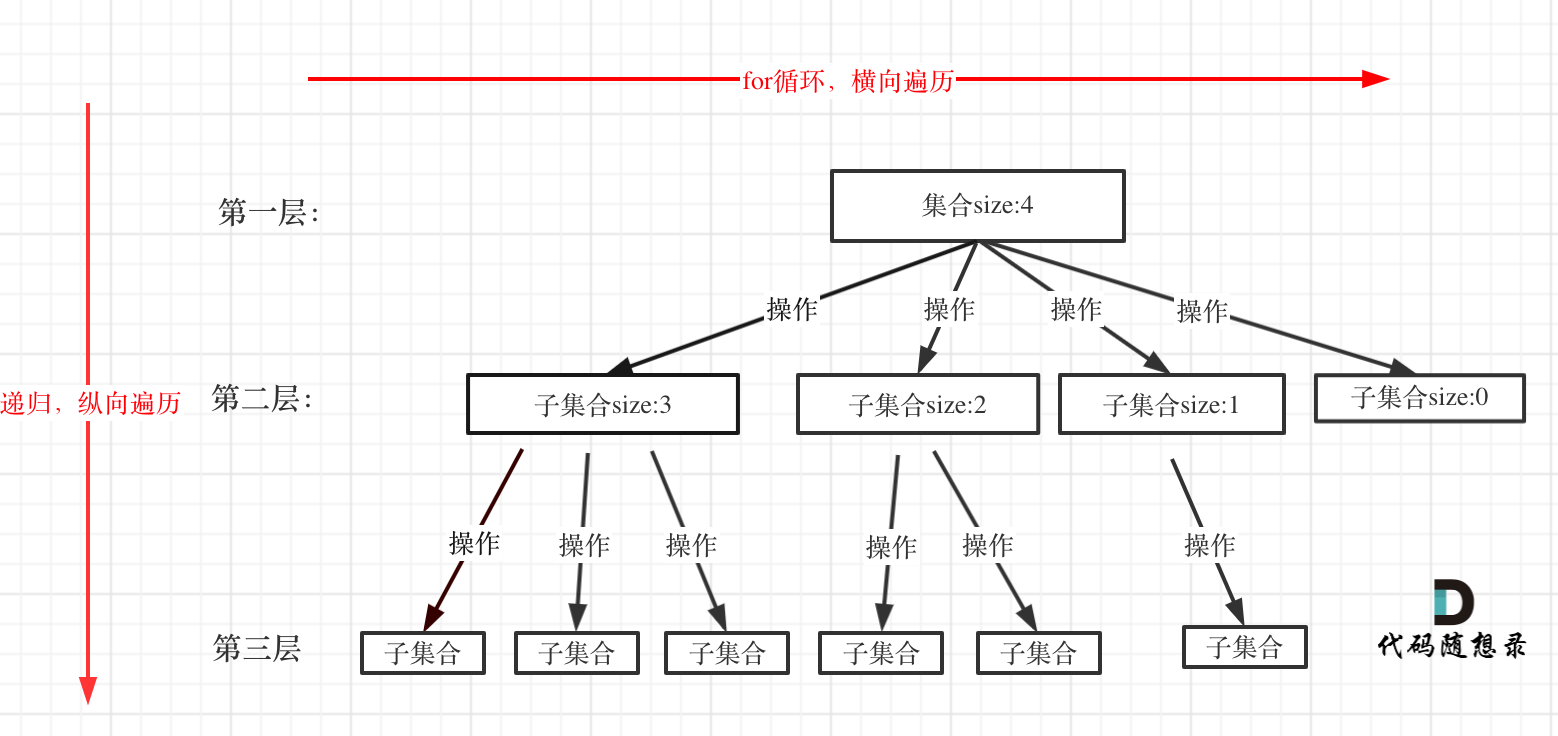
特意举例:集合大小和孩子的数量是相等的!
回溯函数遍历过程伪代码如下:
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
for 循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个 for 循环就执行多少次。
backtracking 这里自己调用自己,实现递归。
大家可以从图中看出 for 循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
分析完过程,回溯算法模板框架如下:
void backtracking(参数) {
if (终止条件) {
存放结果; // y
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
回溯与分治的区别
不一定对
-
回溯更多的是 DFS,自底向上;类似于后序遍历
-
分治更多的先解决了当前层的问题,再去解决下一层的子问题,自顶向下;类似于先序遍历
-
回溯有一种回到当前层来解决问题的感觉,解决当前层的问题需要依赖更深层所提供的信息;而分治的上层则不依赖下层
-
回溯更多的是找到一个集合(路径、排列...),需要遍历空间集,实质上是一种很笨的方法(DFS 嘛)。分治更多的是改变一个序列的排序等等
-
回溯的特色是剪枝;分治的特色是分解后的合并
排序模板
快排
var quickSort func(nums []int, l, r int)
quickSort = func(nums []int, l, r int) {
pivotPos := true // 基准值位置 true为前
i, j := l, r
for i < j {
if !compare(nums[i], nums[j]) {
// 逆序
pivotPos = !pivotPos
nums[i], nums[j] = nums[j], nums[i]
}
if pivotPos {
j--
} else {
i++
}
}
if l < i-1 {
quickSort(nums, l, i-1)
}
if i+1 < r {
quickSort(nums, i+1, r)
}
}