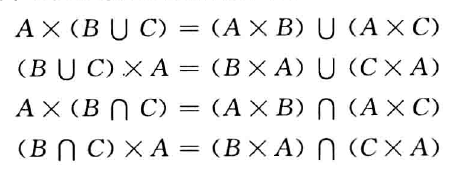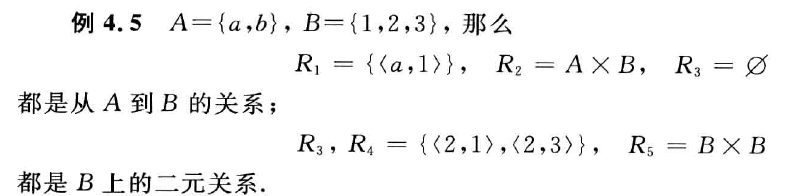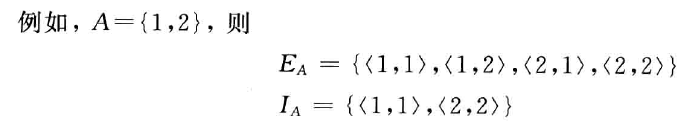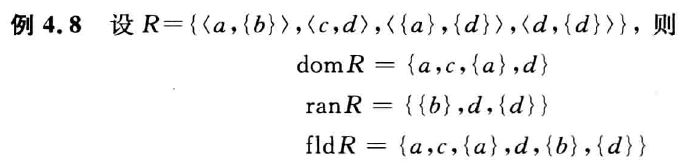关系
两个元素按照一定次序构成的二元组称为一个有序对,记作 <x, y>,区分第一元素和第二元素(即拥有有序性)
设 A,B 为集合,以 A 中元素作为第一元素,B 中元素为第二元素,构成的所有有序对叫做笛卡尔积,记为A×B,即
A×B={<x,y>∣x∈A∧y∈B}
性质
-
A,B 有空集时,笛卡尔积为空集
-
不适合交换律
-
不适合结合律
-
对于并或交运算满足分配律
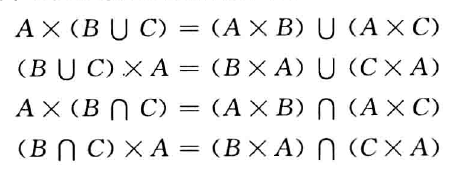 <x1,x2,…,xn>A1×A2×…×An={<x1,x2,…,xn>∣xi∈Ai}
<x1,x2,…,xn>A1×A2×…×An={<x1,x2,…,xn>∣xi∈Ai}
若集合满足以下条件之一:
- 集合非空,它的元素都是有序对
- 集合是空集
则该集合是一个二元关系,简称关系,记作R
如<x,y>∈R,可记作xRy;如<x,y>∈/R,可记作xRy
例

A×B 的任何自己所定义的二元关系叫做从 A 到 B 的二元关系,当 A=B 时则叫做A上的二元关系
。==从 A 到 B 的二元关系近似看作 A×B 的子集==
例
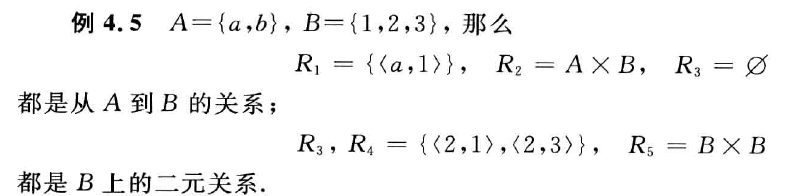
 EA={⟨x,y⟩∣x∈A∧y∈A}=A×A
IA={⟨x,x⟩∣x∈A}
LA={⟨x,y⟩∣x,y∈A∧x<y}A⊆R
DA={⟨x,y⟩∣x,y∈A∧x整除y}B⊆Z∗
R⊆={⟨x,y⟩∣x,y∈A∧x⊆y}
EA={⟨x,y⟩∣x∈A∧y∈A}=A×A
IA={⟨x,x⟩∣x∈A}
LA={⟨x,y⟩∣x,y∈A∧x<y}A⊆R
DA={⟨x,y⟩∣x,y∈A∧x整除y}B⊆Z∗
R⊆={⟨x,y⟩∣x,y∈A∧x⊆y}
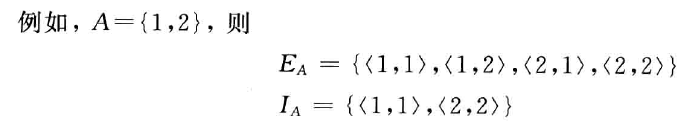

懂的都懂
设R是从A到B的关系,R 的关系矩阵是布尔矩阵MR=(rij)m×n,其中rij=1⇔⟨xi,yj⟩∈R
R的关系图是GR=⟨A,R⟩,其中 A 为 G 的节点集

- 定义域:第一元素的集合,domR
- 值域:第二元素的集合,ranR
- 域:全体元素的集合,fldR
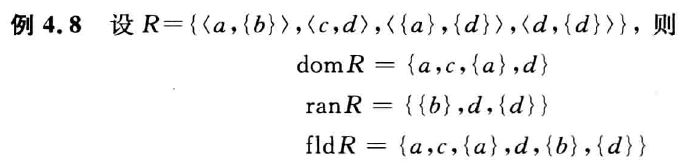 R−1={⟨y,x⟩∣⟨x,y⟩∈R}
R∘S={⟨x,z⟩∣∃y(⟨x,y⟩∈R∧⟨y,z⟩∈S)}
R−1={⟨y,x⟩∣⟨x,y⟩∈R}
R∘S={⟨x,z⟩∣∃y(⟨x,y⟩∈R∧⟨y,z⟩∈S)}


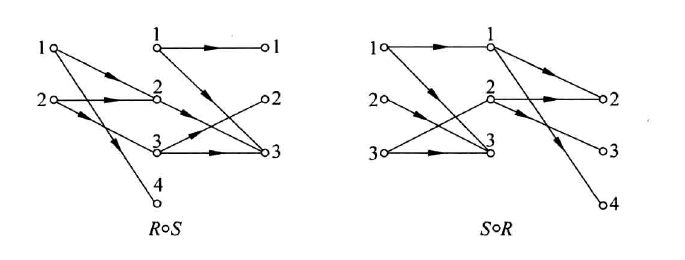
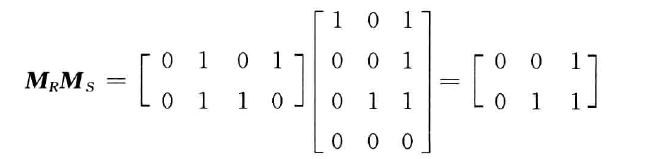
-
定理 1:设F是任意的关系,则
- (F−1)−1=F
- domF−1=ranF,ranF−1=domF
-
定理 2:设F,G,H是任意的关系,则
- (F∘G)∘H=F∘(G∘H)
- ==(F∘G)−1=G−1∘F−1==
-
定理 3:设R为A上的关系,则
- R∘IA=IA∘R=R
设R为A上的关系,则R的 n 次幂的定义为
- R0={⟨x,x⟩∣x∈A}=IA
- Rn+1=Rn∘R
- 设A为n元集,R为A上的关系,则存在自然数 s 和 t,使得 Rs=Rt
- 设R为A上的关系,有
- Rm∘Rn=Rm+n
- (Rm)n=Rmn
- 设R为A上的关系,若存在自然数 s 和 t(s<t),使得Rs=Rt,则
- 对任何k∈N有Rs+k=Rt+k
- 对任何k,i∈N 有 Rs+kp+i=Rs+i,其中 p=t−s
- 令S{Ro,R1,…,Rt−1},则对于任意的q∈N有Rq∈S

设R为A上的关系,有
- 若∀x(x∈A→⟨x,x⟩∈R),则称R在A上自反
- 若∀x(x∈A→⟨x,x⟩∈/R),则称R在A上反自反

自反:对角线全为 1
反自反:对角线全为 0
除空关系外,一个关系不可能同时是自反和反自反的

设R为A上的关系,有
- 若 ∀x∀y(x,y∈A ∧⟨x,y⟩∈R→⟨y,x⟩∈R),则称R在A上对称
- 若 ∀x∀y(x,y∈A ∧⟨x,y⟩∈R∧⟨y,x⟩∈R→x=y),则称R在A上反对称


对称:每个元素要么自我相等要么两两相反
反对称:每个元素不能两两相反(但可以自我相等)
一个关系可以同时是对称和反对称的

设R为A上的关系,有
∀x∀y∀z(x,y,z∈A∧⟨x,y⟩∈R∧⟨y,z⟩∈R→⟨x,z⟩∈R)
则称R是传递的

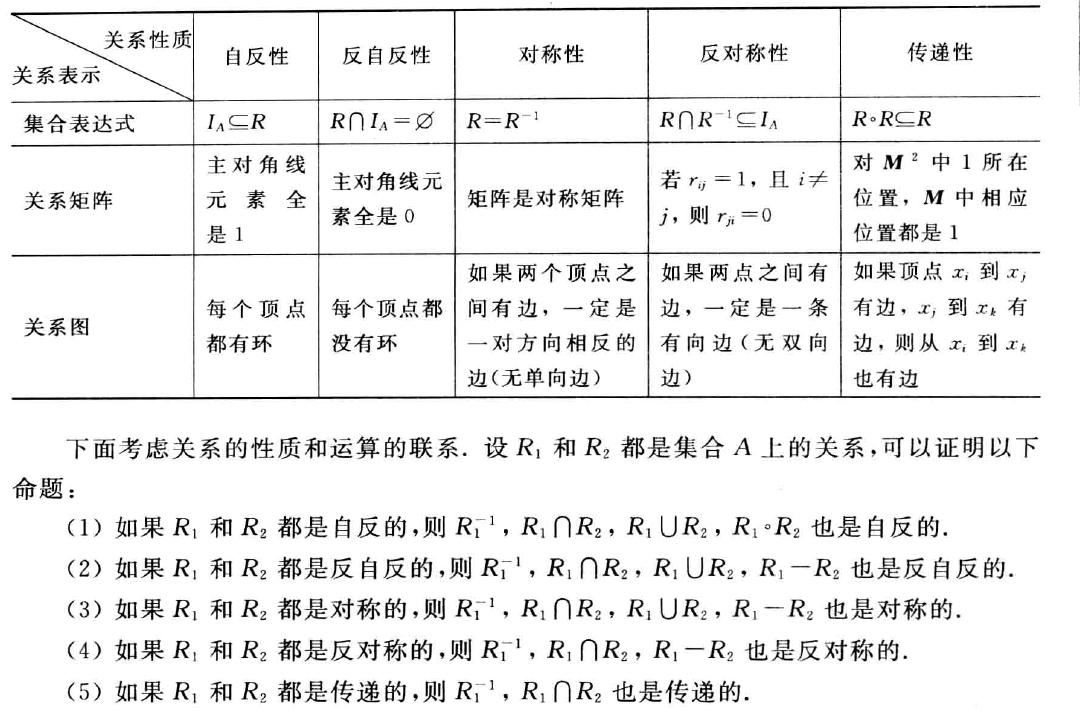
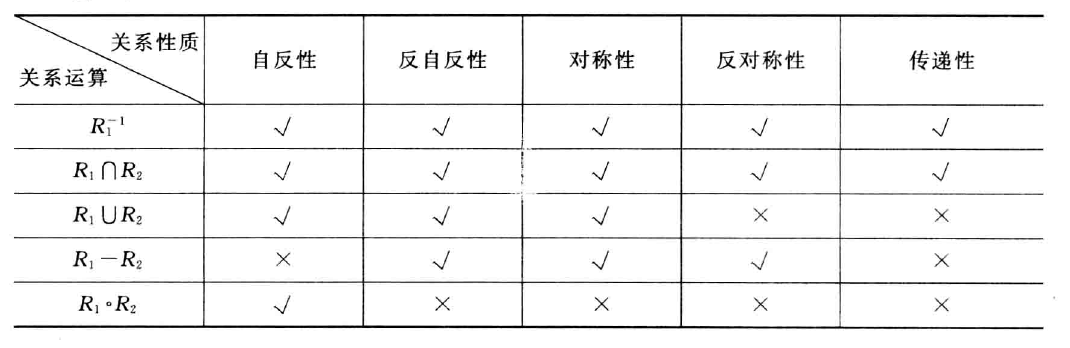
设R为A上的关系,若R不具有某种性质,可以通过在R中加入最少数量的有序对来补充R,使其具有某种性质
设R为非空集合A上的关系,R的自反(对称或传递)闭包是A上的关系R′,使R′满足以下条件
- R′是自反的(对称的或传递的)
- R⊆R′
- 对A上任何包含R的自反(对称或传递)关系R′′有R′⊆R′′
自反闭包:r(R)
对称闭包:s(R)
传递闭包:t(R)
想使一个关系拥有某一性质,向其中尽量少地添加一些有序对,形成的新关系称为闭包。
设R为A上的关系,有
- r(R)=R∪R0
- s(R)=R∪R−1
- t(R)=R∪R2∪R3∪…
用矩阵关系表示
- Mr=M+E
- MS=M+M′
- Mt=M+M2+M3+…
用图关系表示
- Gr:在图G中每一个缺少环的结点都加一个环
- Gs:将G中的单向边变成双向边
- Gt:
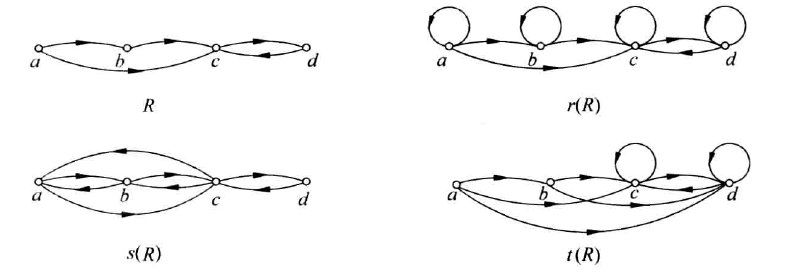


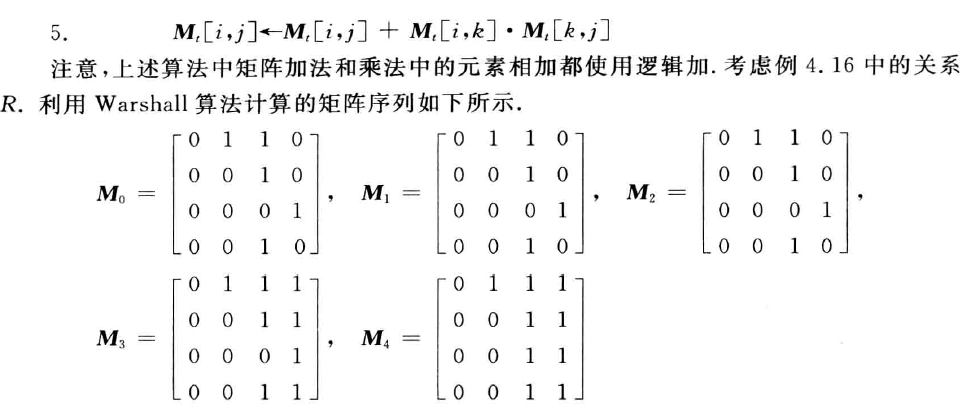
设R为非空集合A上的关系,若R是自反的,对称的,传递的,则称R为A上的等价关系,
对于任何元素 x,y∈A,若xRy,则称 x, y 等价,记为x∼y
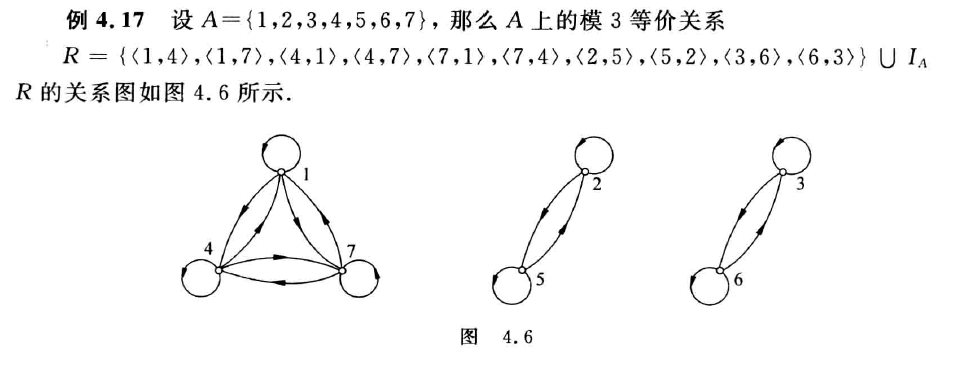
按某一等价关系,将 A 的元素划分成若干个子集,彼此等价的元素被分在同一个子集里,这些子集称作这个等价关系产生的等价类。记作[x]

- ∀x∈A,[x]是A的非空子集
- ∀x,y∈A,如果xRy,则[x]=[y]
- ∀x,y∈A,如果xRy不成立,则[x]与[y]不交
- ⋃x∈A[x]=A,即A中元素构成的所有等价类的并集等于A
A上的全体等价类构成的集合称作A关于等价关系R的商集,记作A/R,即
A/R={[x]R∣x∈A}

设A为非空集合,若A的子集族 π(π⊆P(A))满足下面条件
- ∅∈/π(无空集)
- ∀x∀y(x,y∈π∧x=y→x∩y=∅)(元素无公共部分)
- ⋃x∈πx=A(拼起来是完整的)
则π称是A的一个划分,称π中的元素为A的划分块

- 商集A/R就是A的一个划分,所以又可以定义商集R
R={⟨x,y⟩∣x,y∈A∧x与y在π的同一划分块中}
非空集合A上的自反、反对称和传递的关系称为A上的偏序关系,简称偏序,记作⪯
若⟨x,y⟩∈⪯,则记作x⪯y,读作 x “小于等于” y
设 R 为非空集合 A 上的偏序关系,∀x,y∈A,若x⪯y∨y⪯x,则称 x 与 y 可比
设R为非空集合A上的偏序关系,若R是反自反的和传递的,则称R是A上的拟序关系,简称为拟序,记作≺

设R为非空集合A上的偏序关系,∀x,y∈A,x 与 y 都是可比的,则称R为全序关系,简称全序(或线序)
设R为非空集合A上的偏序关系,∀x,y∈A,若x≺y且不存在z∈A使得x≺z≺y,则称 y覆盖x
定义偏序关系R的一个子关系——覆盖关系T
T={⟨x,y⟩∣⟨x,y⟩∈R且y覆盖x}
T的自反传递闭包rt(T)就等于R
集合A和A上的偏序关系⪯一起叫做偏序集,记作⟨A,⪯⟩

定义
利用偏序自反、反对称、传递性简化的关系图
特点
- 每个结点没有环
- 两个联通结点之间的序关系通过结点位置的高低表示,位置低的元素顺序在前
- 具有覆盖关系的两个结点之间连边

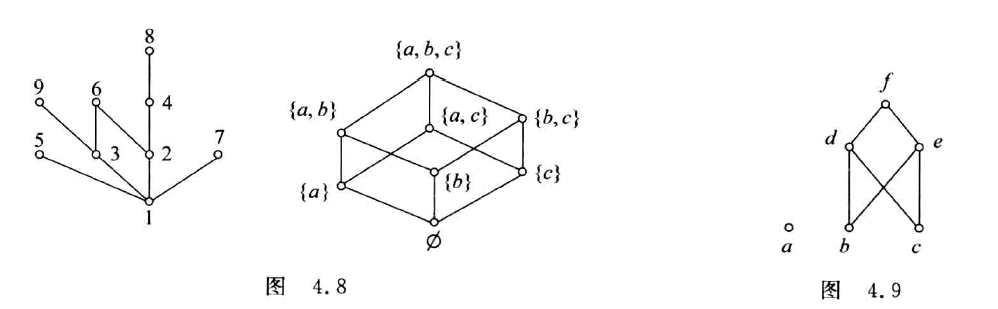
设⟨A,⪯⟩为偏序集,B⊆A,y∈B
- 若∀x(x∈B→y⪯x)成立,则称y为B的最小元
- 若∀x(x∈B→x⪯y)成立,则称y为B的最大元
- 若∀x(x∈B∧x⪯y→x=y)成立,则称y为B的极小元
- 若∀x(x∈B∧y⪯x→x=y)成立,则称y为B的极大元
有性质如下
- 对于有穷集,极小元和极大元一定存在,还可能存在多个
- 最小元和最大元不一定存在,如果存在一定唯一
- 最小元一定是极小元,最大元一定是极大元
- 孤立结点既是极小元,也是极大元
设⟨A,⪯⟩为偏序集,B⊆A,y∈A
- 若∀x(x∈B→x⪯y)成立,则称y为B的上界
- 若∀x(x∈B→y⪯x)成立,则称y为B的下界
- 令C={y∣y为B的上界},则称C的最小元为B的最小上界或上确界
- 令D={y∣y为B的下界},则称D的最大元为B的�最大下界或下确界
有性质如下
- 上界,下界,最大下界,最小上界不一定存在
- 如果下界,上界存在,也不一定是唯一的
- 最大下界,最小上界如果存在,则是唯一的
- 子集B的最小元就是他的最大下界,最大元就是他的最小上界;反之不对
理解
最小元素就是在子集中处于最低层且每个元素通过图中路径都可以找到它且它的下面没有元素。
极大元素就是在子集中它的上面没有元素。
极小元素就是在子集中它的下面没有元素。
(记住:这里如果是子集,应当将子集当成一个单独的整体,而不受全集的影响。)
上届:所有子集内的元素沿着路径向上都可以找到的元素(这里包括子集和子集以外的元素)。根据上面所说的话,我们可以断定上届也可以是子集内的元素。
下届:所有子集内的元素沿着路径向下都可以找到的元素(这里包括子集和子集以外的元素)。根据上面所说的话,我们可以断定下届也可以是子集内的元素。
上确界:这里我们可以将上届元素看成一个独立的整体,而上确界就是这个集合的最小元,我们称为最小上届。根据上面所说的话,我们可以断定上届也可以是上确界。
下确界:这里我们可以将下届元素看成一个独立的整体,而下确界就是这个集合的最大元,我们称为最大下届。根据上面所说��的话,我们可以断定下届也可以是下确界。
设⟨A,⪯⟩为偏序集,B⊆A
- 若∀x,y∈B,x与y都是可比的,则称B是A中的一条链,B中的元素个数称为链的长度。
- 若∀x,y∈B,x=y,x与y都是不可比的,则称B是A中的一条反链,B中的元素个数称为反链的长度。

有定理
- 设⟨A,⪯⟩为偏序集,若A中最长链的长度为n,则该偏序集可以分解为n条不相交的反链