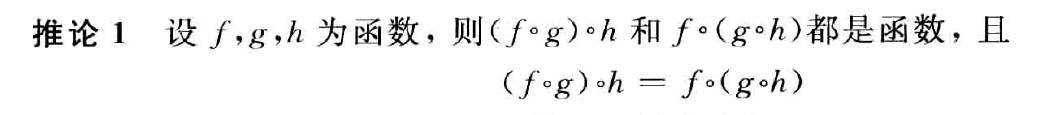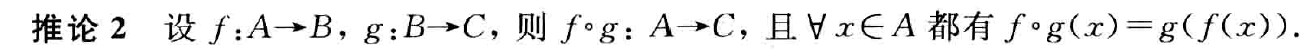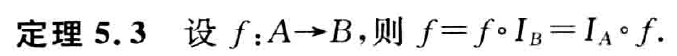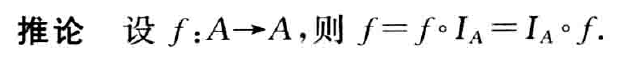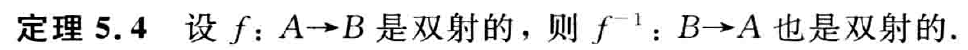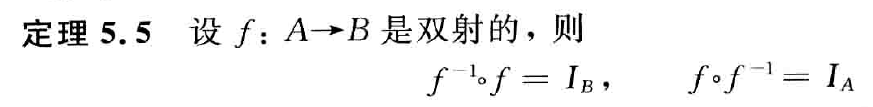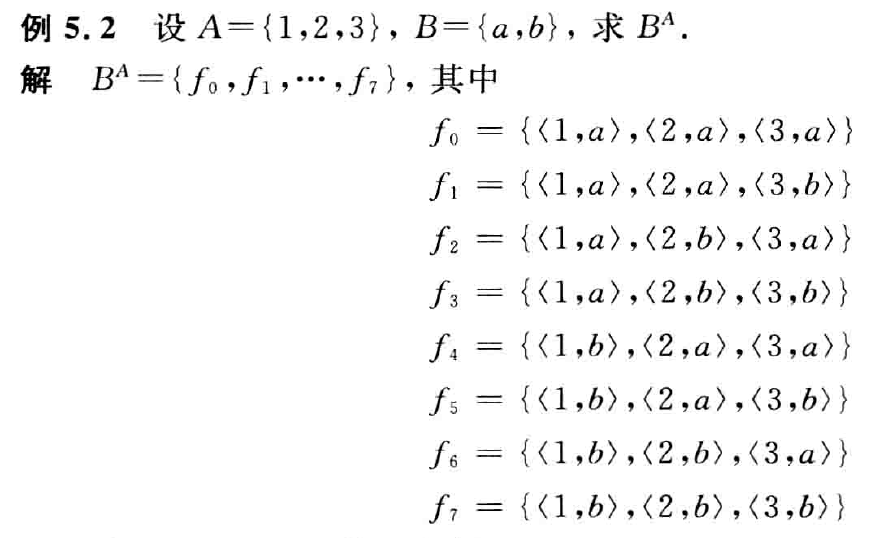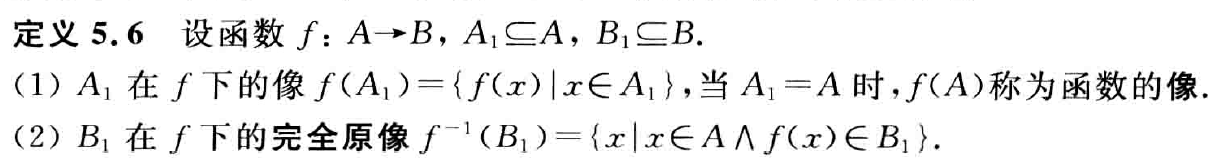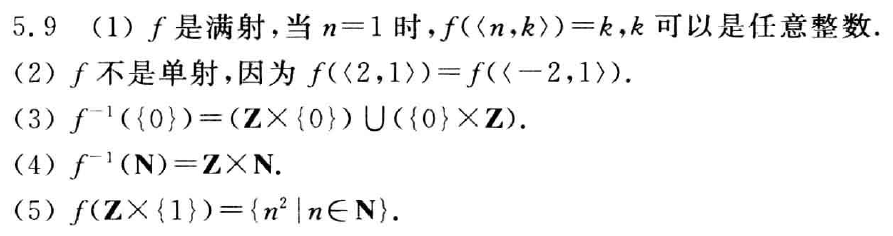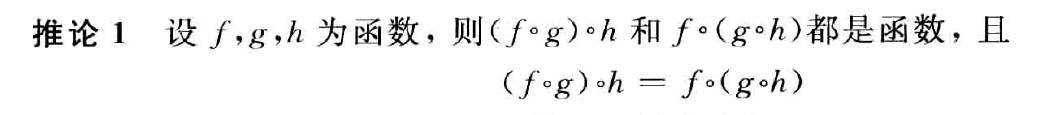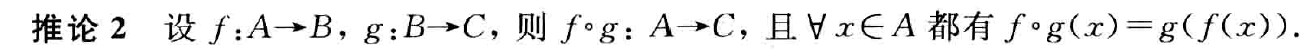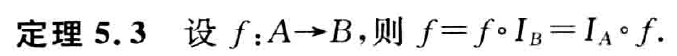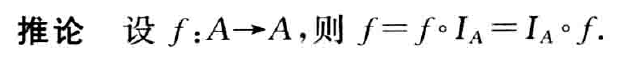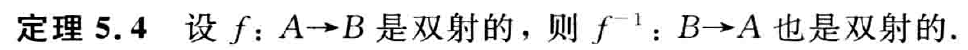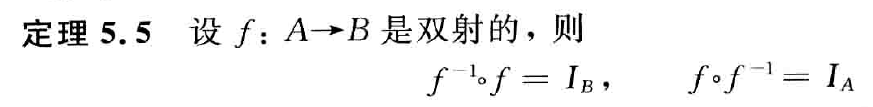函数
设 f 为二元关系,若对于任意 x∈domf,都存在唯一的 y∈ranf,使得 xfy 成立,则称 f 为函数(或映射),这时也称 y 为 f 在 x的 值,记作 y=f(x)
设f,g为函数,则
f=g⇔f⊆g∧g⊆f
根据上述定义,若f和g相等,一定满足下面两个条件
- domf=domg,定义域相等
- ∀x∈domf=domg 都有 f(x)=g(x),值相等
设A,B为集合,若
f为函数,domf=A,ranf⊆B
则称f为从A到B的函数,记作f:A→B


所有从A到B的函数的集合记作 BA,符号化表示为
BA={f∣f:A→B}
若 ∣A∣=m,∣B∣=nm,n=0,则 ∣BA∣=nm
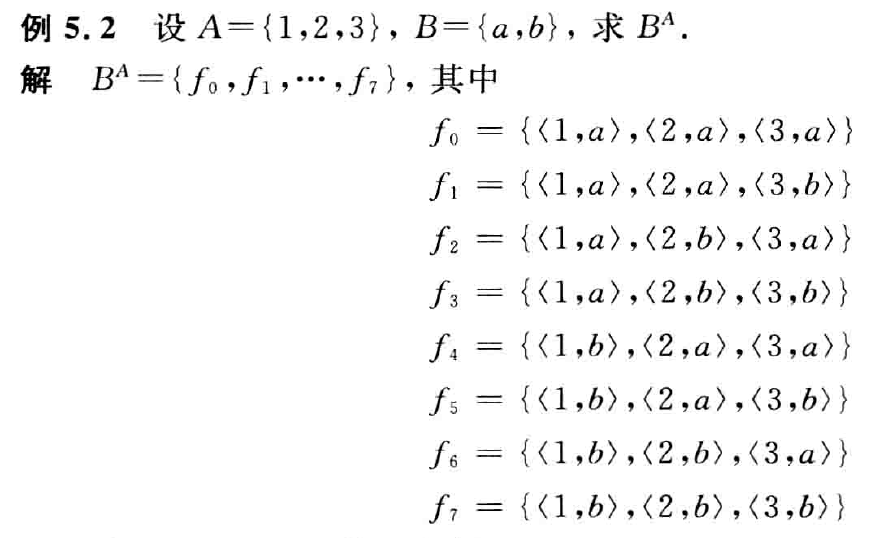
- 设 f:A→B,若存在 c∈B 使得对所有的 x∈A 都有 f(x)=c,则称 f:A→B 是常函数

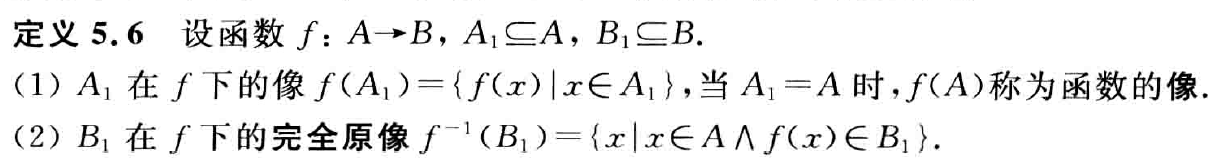
- 像:一些 f(x) 的集合
- 完全原像:一些 x 的集合


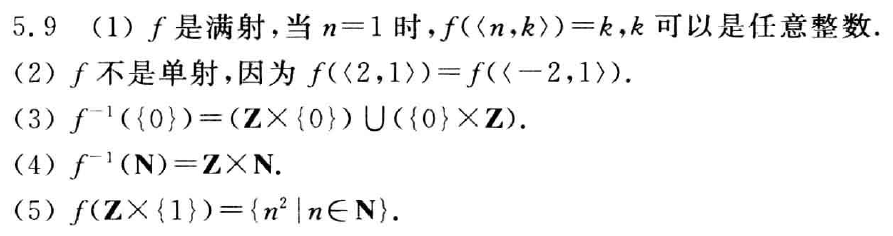

。满射:大家都有对象
。单射:一夫一妻
。双射:一夫一妻,大家都有对象

单射一定是单调的,满射的值域一定等于 B