基本概念

有了数据，通过某种学习算法，得到模型，进行预测。

• 数据

  • 数据集（Data Set）：一组记录的集合（一堆西瓜）
  • 样本（Sample）：一个对象或事件的描述（一个西瓜）
  • 特征向量（Feature Vector）：各种属性（Attribute）张成的一个样本空间（Sample Space），各种属性的总合就是维度（Dimensionality）

• 算法

  • 学习（Learning）或训练（Training）

• 模型（学习器 Learner）

  • 有监督学习
    • 分类（Classification）：预测离散值，二分类，多分类
    • 回归（Regression）：预测连续值
  • 无监督学习
    • 聚类（Clustering）：机器自动形成簇（Cluster），对应一些潜在的分类

• 预测

  • 测试（Testing）
  • 测试样本（Testing Sample）
  • 泛化能力（Generalization）：模型适用于新样本的能力

• 假设空间：将学习过程看作一个在所有假设（Hypothesis）组成的空间中进行搜索的过程，搜索目标是找到与训练集匹配的假设

• 归纳偏好：机器学习算法在学习过程中对某种类型假设的偏好

  原理：奥卡姆剃刀

模型评估与选择

术语

• 过拟合（Overfitting）：将训练样本自身特点当作了潜在样本的一般性质，导致泛化能力下降

• m：样本数量；Y：正确结果；Y’：预测结果；a：错误数

• 性能度量

  • 错误率（Error Rate）：$E=\cfrac{a}{m}$
  • 精度（Accuracy）：$1-E$
  • 误差（Error）：$|Y-Y'|$

• 数据集

  • 训练集（Training Set）：用于训练模型的集数据集
  • 测试集（Testing Set）：用于测试模型的数据集
  • 验证集（Validation Set）：用于评估测试的数据集，用于调参（Parameter tuning）

  步骤：用训练集训练->用验证集看结果->调参->循环。最后在测试集上看结果

一种训练集，一种算法

测试集的选择方法

1. 留出法

   将数据集 D 划分为互斥集合，训练集 S 与测试集 T，用 T 来评估和测试误差。

   要求

   • 数据划分时保持数据分布的一致性，如分层采样（Stratified Sampling）
   • 通常三七分，二八分（大部分数据用来训练），或进行多次随机划分，训练出多个模型，最后取平均值。

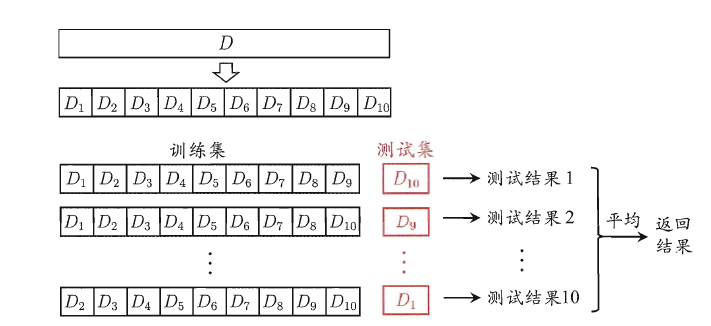
2. k折交叉验证法

   将数据集 D 分成 k 份，每次以 k-1 个子集作为训练集 S 来训练，用余下的那一个子集用来测试，重复 k 次取平均值。

   缺点：太慢太麻烦

   

3. 自助法

   在数据集 D 中随机挑选样本放入训练集 S 中，再放回，重复 m 次（自助采样）。

   此时，D 中部分样本会在 S 中多次出现，部分样本不会出现，不被采到的概率为$(1-\cfrac{1}{m})^m$，取极限约为 36.8%，将不出现的样本作为测试集 T，这样的测试结果称为包外估计（out-of-bagestimate）。

   缺点：改变了初始数据集的分布，引入估计偏差。

性能度量（Performance Measure）

基本公式

给定样例集$D=\{(x_1,y_1),(x_2,y_2),\ldots,(x_m,y_m)\}$，其中$y_i$是示例$x_i$的真实标记，要评估学习器$f$的性能，就要把学习器的预测结果$f(x)$与真实标记$y$进行比较。

• 均方误差

$$E(f;D)=\cfrac{1}{m}\sum\limits_{i=1}^{m}(f(x_i)-y_i)^2$$

• 对于数据分布$\cal{D}$和概率密度函数$p(\cdot)$，均方误差可描述为

$$E(f;D)=\int_{x\sim D}(f(x)-y)^2p(x)dx$$

• 错误率

$$E(f;D)=\cfrac{1}{m}\sum\limits_{i=1}^{m}\Bbb{I}(f(x_i)\neq y_i)$$

• 错误精度

$$acc(f;D)=1-E(f;D)$$

查准率与查全率

• 混淆矩阵

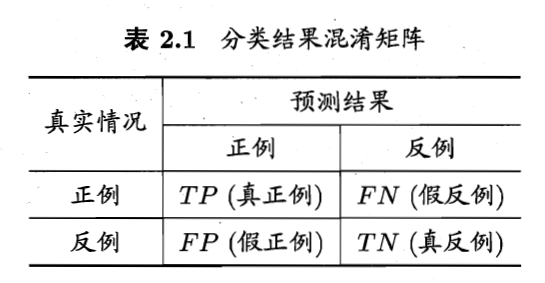
• 查准率$P$（Precision）：预测为正例的结果中有多少是对的，阈值（Threshold）较大（谨慎），查准率往往会高

$$P=\cfrac{TP}{TP+FP}$$

• 查全率$R$（Recall）：真正的正例有多少被预测出来了，阈值较小（宽松），查全率往往会高

$$R=\cfrac{TP}{TP+FN}$$

最优阈值的确定

• 选取平衡点（Break-Even Point），简称 BEP
• $F1$ 度量（P 与 R 的调和平均数）

$$\cfrac{1}{F1}=\cfrac{1}{2}(\cfrac{1}{R}+\cfrac{1}{P}) \\ F1=\cfrac{2\times P\times R}{P+R}=\cfrac{2\times TP}{样例总数+TP-TN}$$

​ 与算术平均与几何平均相比，调和平均更重视最小值

• $F_\beta$ 度量（加权调和平均）

$$\cfrac{1}{F_\beta}=\cfrac{1}{1+\beta^2}(\cfrac{1}{P}+\cfrac{\beta^2}{R}) =\cfrac{(1+\beta^2)\times P\times R}{(\beta^2\times P)+R}$$

​ $\beta$度量了查全率相对于查准率的重要性，$\beta>1$时查全率影响更大；$\beta<1$时查准率影响更大

n 个二分类实现的多分类问题

• 先分别计算，再求平均值

  有$(P_1,R_1),(P_2,R_2),\ldots,(P_n,R_n)$

  • macro-P 宏查准率：$macro-P=\cfrac{1}{n}\sum\limits_{i=1}^n P_i$
  • macro-R 宏查全率：$macro-R=\cfrac{1}{n}\sum\limits_{i=1}^n R_i$
  • macro-F1 宏 F1：$macro-F1=\cfrac{2\times macroP\times macroR}{macroP+macroR}$

• 先平均再计算

  • macro-P 宏查准率：$micro-P=\cfrac{\overline{TP}}{\overline{TP}+\overline{FP}}$

  • macro-R 宏查全率：$micro-R=\cfrac{\overline{TP}}{\overline{TP}+\overline{FN}}$

  • macro-F1 宏 F1：$micro-F1=\cfrac{2\times microP\times microR}{microP+microR}$

一种训练集，多种算法

P-R曲线

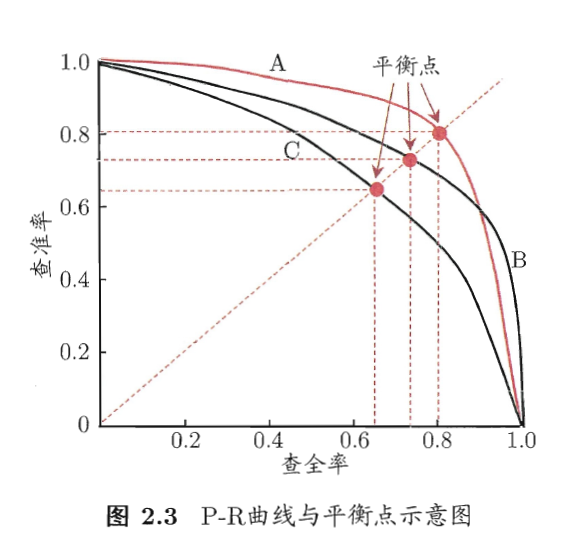
要比较 ABC 三个模型的好坏

• 首先确定 A 和 B 优于 C，AB 间由于交叉不好确定
• 对于 AB
  • 法一：比较面积，但不易估算
  • 法二：$F1$
  • 法三：$F\beta$

ROC 与 AUC